三角形の合同の証明① 下の図で,ab=ac,−bad=−cad である。このとき,¼abd×¼acd で あることを右のように証明した。下線部 をうめて,証明を完成させなさい。 三角形の合同の証明② 下の図で,am=cm,bm=dm であ る。このとき,ab=cd であることを右 合同式(mod)とは? 性質の証明や計算問題の解き方 21年2月19日 この記事では、「合同式 」についてわかりやすく解説していきます。 合同式の性質や解き方、不定方程式との関係なども説明していきますので、ぜひこの記事を通してマスターして3-8.平面図形 合同の証明 複合問題ほか 11年度出題 問1 図のように,正三角形abcの辺bc上に点dをとり,adを1辺とする正三角形adeをつくる。また,辺deと辺acの 交点をfとする。次の(1),(2)に答えなさい。 (青森県 後期 11年度)
Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 合同の証明 働きアリ
直角三角形 合同 証明 問題
直角三角形 合同 証明 問題-カテゴリ: @ 平面(証明メイン) 相似 証明 中学数学 高校入試 三平方の定理 スポンサーリンク このブログは「高校入試 難問」や「高校入試 数学 良問」などで検索して来られる方が多いです。 ということで,久々に芸術的な,中学数学の問題をご 証明の問題プリント 証明の問題は「図形の性質(中学2年内容)」「相似(中学3年内容)」「円(中学3年内容)」で作成しています。 自分が学習している内容から始めてください。 毎日1枚ずつ取り組むと1か月ぐらいになるかと思います。 毎日しっかりと解くことで,1か月後には本当に証明ができるようになっているはずです。 苦手で最初は嫌かもしれ



1
三角形の合同条件 合同の証明 二等辺三角形の証明 正三角形、正方形を 利用した合同の証明 直角三角形の 合同の証明 等積変形な問題が,21の都立西にあったのでご紹介します。 問1,問2中2の図形証明分野習った後に解ける 問3相似習った後に解ける 芸術的な難問高校入試 第52回 「平行四辺形の超難しい証明」 出典:令和3年度 都立西高校(独自作成校) 過去問 数学だけど、しっかりとした手順を身につけてもらえれば、すっごく簡単に解くことができるようになるよ! 今回の記事では、三角形の合同を証明する問題を基礎からみっちりと解説していくね! それでは、次の問題を利用して証明の書き方について解説していきます。 下の図で、AB=AD、BC=DCならば、 ABC≡ ADCとなることを証明し
正三角形の合同証明 正三角形を含む図形の三角形の合同証明の問題です。 正三角形は 三辺が等しい 3つの角度がすべて等しい (すべて60°) であることを利用して、等しい辺、等しい角を探していきます。 等しい辺、角をすべて書き込んでいけば、証 三角形の合同の証明応用問題 ABCで、辺AB、辺ACをそれぞれ1辺とする正三角形 ABD、 ACEを、 ABCの外側につくります。 このとき、BE=DCであることを証明しなさい。 三角形の合同の証明応用問題の解答 ABEと ADCにおいて ABDは正三角形なので、AB=AD① ACEは正三角形なので、AE=AC① 正三角形の1つの内角は60°だか右図の abc と def が合同であることを証明した い。ab=de,bc=ef であることがわかっているとき, あと1 つ,どのようなことをつけ加えれば合同であるこ とが証明できるか。適切なものを次のア~エから2 つ選 び,記号を書け。
今回は中2の合同の証明問題です。折り返しの問題です。それではどうぞ。 下の図のように, abよりadが長くなるような長方形abcdを, 対角線acで折り返します。折り返したあとのbの位置をe, ecとadとの交点をfとするとき, 次の問いに答えなさい。証明問題を解く上で覚えておきたいポイント! 図形の証明問題に関して覚えておきたいポイントを説明します。 図形の証明問題は基本的に、三角形の合同条件などの「条件」を「根拠」を挙げて示す、というパターンです。 そのため慣れてしまえばワン三角形の合同の証明 基本問題1 図でAC=DB, ∠ACB=∠DBCのとき, ABC≡ DCBを証明せよ。 A B C D 図でAB=DC, AC=DBのとき, ABC≡ DCBを証明せよ。 A B C D 右の図でAC//BD, AD//BCのとき, ABC≡ BADとなることを証明せよ。 A B C D 解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。 解説リクエスト 平行と合同 要点 平行線の錯角と同位角 内角の和、外




世界一わかりやすい数学問題集中2 4章 平行と合同と証明



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
数学4.平面図形 3.合同の証明 複合問題ほか 08年度 数学4.平面図形 3.合同の証明 複合問題ほか 09年度 数学4.平面図形 3.合同の証明 複合問題ほか 10年度 数学4.平面図形 3.合同の証明 複合問題ほか 11年度 公立高校入試 過去問 数学 中学生 数学 合同 中学生 数学 合同の証明 在宅学習 在宅学習で高校入試対策 在宅学習で高校受験対策 在宅学習図形の証明問題の解き方と証明の書き方のポイントをお伝えします。 中学の数学での図形の証明問題は合同か相似を利用することがほとんどです。 長さが等しいことや角度が等しいことを示すのも合同か相似を証明してからになります。 こ合同の証明2 1 右の図でBDは∠ADCの二等分線で、 AD=BD、∠CAD=∠CBDである。 このとき AED≡ BCDとなることを証明しなさい。 2 図で点Dは辺ABの中点で、DF//BC、DF=BEとなって いる。 このとき ADF≡ DBEを証明せよ。
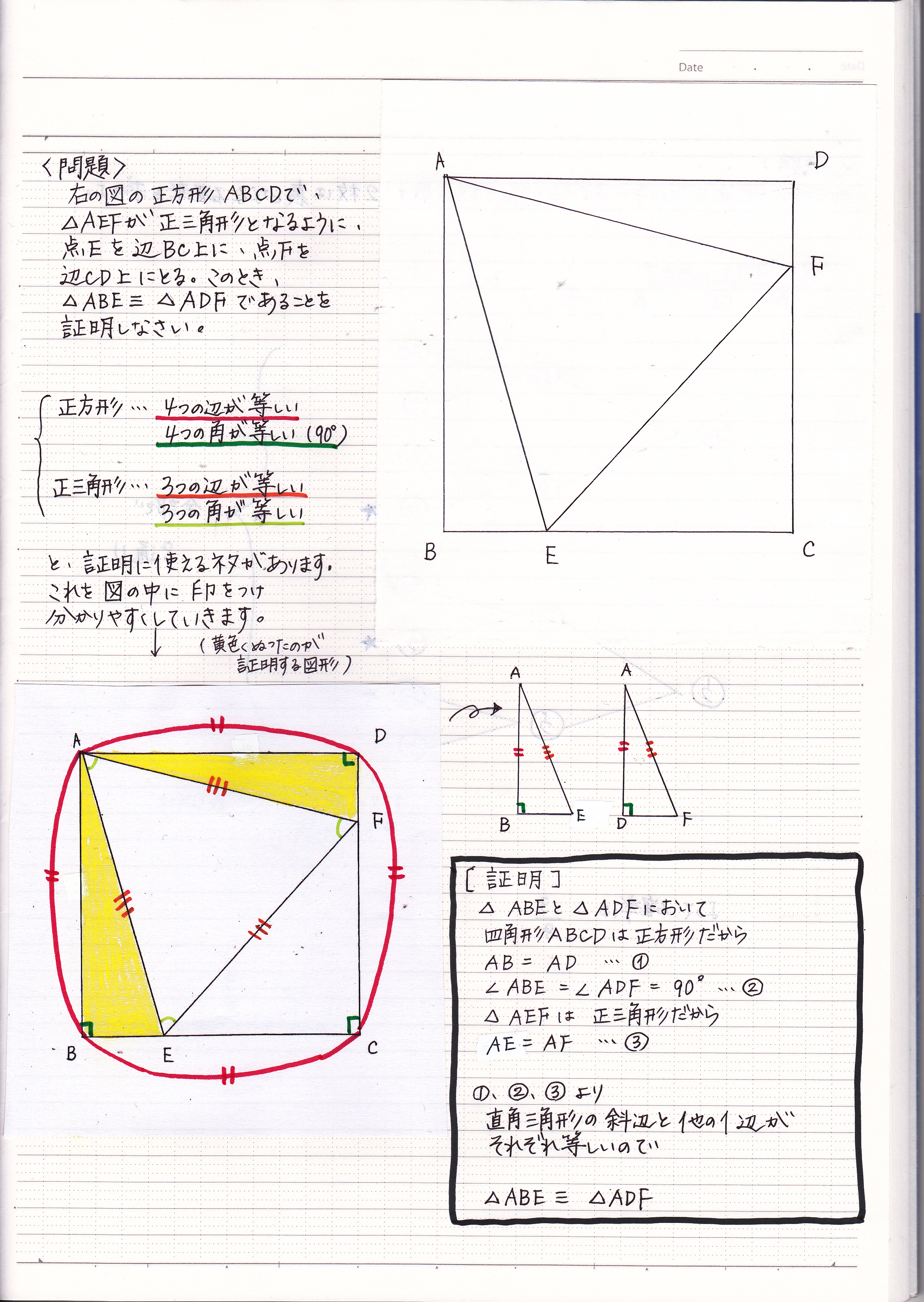



直角三角形の合同条件を使った証明問題の解き方 2 現役塾講師のわかりやすい中学数学の解き方



中2数学 証明の基礎 仮定 結論 三角形の合同を利用 まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
証明(合同) 1枚ずつ印刷 証明 練習用シート 証明 練習用シート(フリー) 「三角形の合同の証明」の手順をつかむための練習シートです。 abc、 defに長さや角度、記号などを自由に書き込んで、証明の問題を作ってご利用くださいませ。三角形の合同条件 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい これから証明問題へ進んでいく上で 必要となってくるものなので ぜーーーーったいに覚えておきましょう! また、合同な基本、「合同」の条件は、 ① 全ての辺の長さが同じ 、 かつ ② 全ての角の大きさが同じ という事実を集められれば、「証明」ですね! 例えば、 なので、 辺AB = 辺DE ① なので、 辺BC = 辺EF ② なので、 辺CA = 辺FD ③ なので、 ∠x = ∠r ④ なので、 ∠y = ∠s ⑤ なので、 ∠z = ∠t ⑥ ∴ ①②③④⑤⑥より 「全ての辺の長さが等しく、 全ての角の大きさが等しい」ので、 ← 「条件」で



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor



头条问答 离职证明是否可以写 严重违反管理制度 不能胜任工作 等此类离职原因 为什么 赵胖说职场的回答 0赞
高校受験に出題される合同の証明問題は、まず間違いなく三角形の合同の証明です。 三角形の合同の証明の 「パターン」をしっかりおさえる ことが、証明問題を解くことのポイントになり平行と合同 角度基礎1 角度基礎2 内角・外角 平行線の錯角・同位角 確認問題 平行線の錯角・同位角 基本問題 平行線の錯角・同位角 標準問題 角度1 角度2 角度3 三角形の合同条件 三角形の合同条件2 三角形の合同の証明 基本問題1 三角形合同の証明1 三角形の合同証明2 三角形の合同証明3 三角形の合同証明4 三角形の合同証明5 平行線の証明 三角形の合同証明6 実は 「図形の証明問題」はさほど難しくはありません 。 コツを掴むと「間違い探し」のような楽しい問題になるんですね。 そのためには、 図形の証明で使う最低限の知識 (図形の性質、合同条件等)を頭に叩き込んで下さい。 大した量ではありません
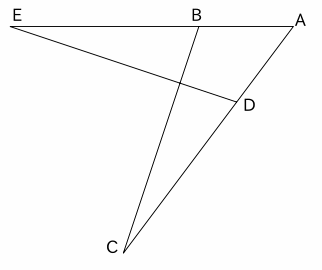



合同の証明6




Lwsjascgsamd6m
図形の証明問題 ってむずかしいよね。 図形の面積を計算する問題とは ちょっと違うタイプ。 苦手な中学生も多いはずだ。 今日はそんな苦手をなくすために、 中2数学図形の証明問題を攻略できる6つのコツ っていう記事をかいてみたよ。今回は、中2で学習する証明問題の単元から 平行四辺形の証明問題について取り上げていくよ! 平行四辺形の証明問題とは、大きく分けて以下の2つだね 平行四辺形の性質を利用した合同の証明;合同証明3 pcが線分abの垂直二等分線のとき apc≡ bpcとなることを証明しなさい。 a b c p 図でoはabの中点、∠oca=∠odbのとき aoc≡ bodとなることを証明せよ。




世界一わかりやすい数学問題集中2 4章 平行と合同と証明



二手挖掘机买卖合同免费下载 二手挖掘机买卖合同范本下载电子版 乐游网手机下载站
この記事では、「合同」についてわかりやすく解説していきます。 三角形の合同条件や証明問題の解き方も説明していくので、ぜひマスターしてくださいね! 目次合同とは?合同の記号合同の性質三角形の合同条件① 3 組の辺がそれ三角形の合同条件:合同の証明問題と解き方のコツ 中学数学で学ぶ図形の問題として、三角形の合同条件があります。 どのようなとき、三角形の形がまったく同じになるのか学ぶのです。 また三角形の合同条件を学んだあと、必ず学ぶのが合同の証明です。 2つの三角形について、合同であることを証明する問題が出されるのです。 数学の問題の中では、証明を



头条问答 自己公司最近出了一项规定 如果员工自愿离职 公司不给开解除劳动合同证明 这合法吗 该怎么办 134个回答



关于申请google Adsense合作证明申请 Google Adsense社群




合同の証明 清水塾




合同の証明 清水塾




国家新闻出版广电总局 关于作品登记和著作权合同备案有关问题的复函 中国音像著作权集体管理协会




持续发酵 中国足协谴责耐克 保留进一步处理同耐克合同的权力 21经济网




解除劳动合同证明word模板下载 熊猫办公




中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット




招投标必须要注意的问题事项 如何对策 谈资质



方万律师事务所



1




中学2年数学練習問題 図形の合同証明の復習と定期テスト対策問題




証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ



疑似伪造合同 证明材料
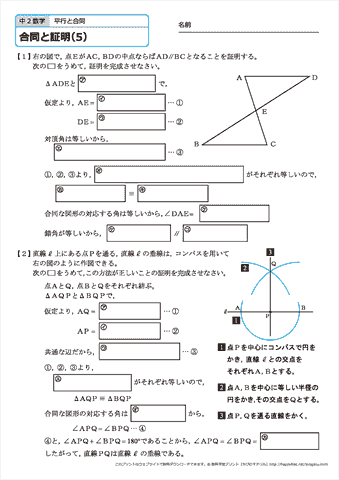



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
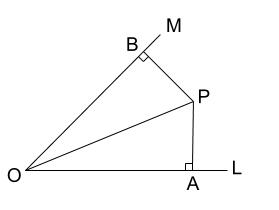



中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su
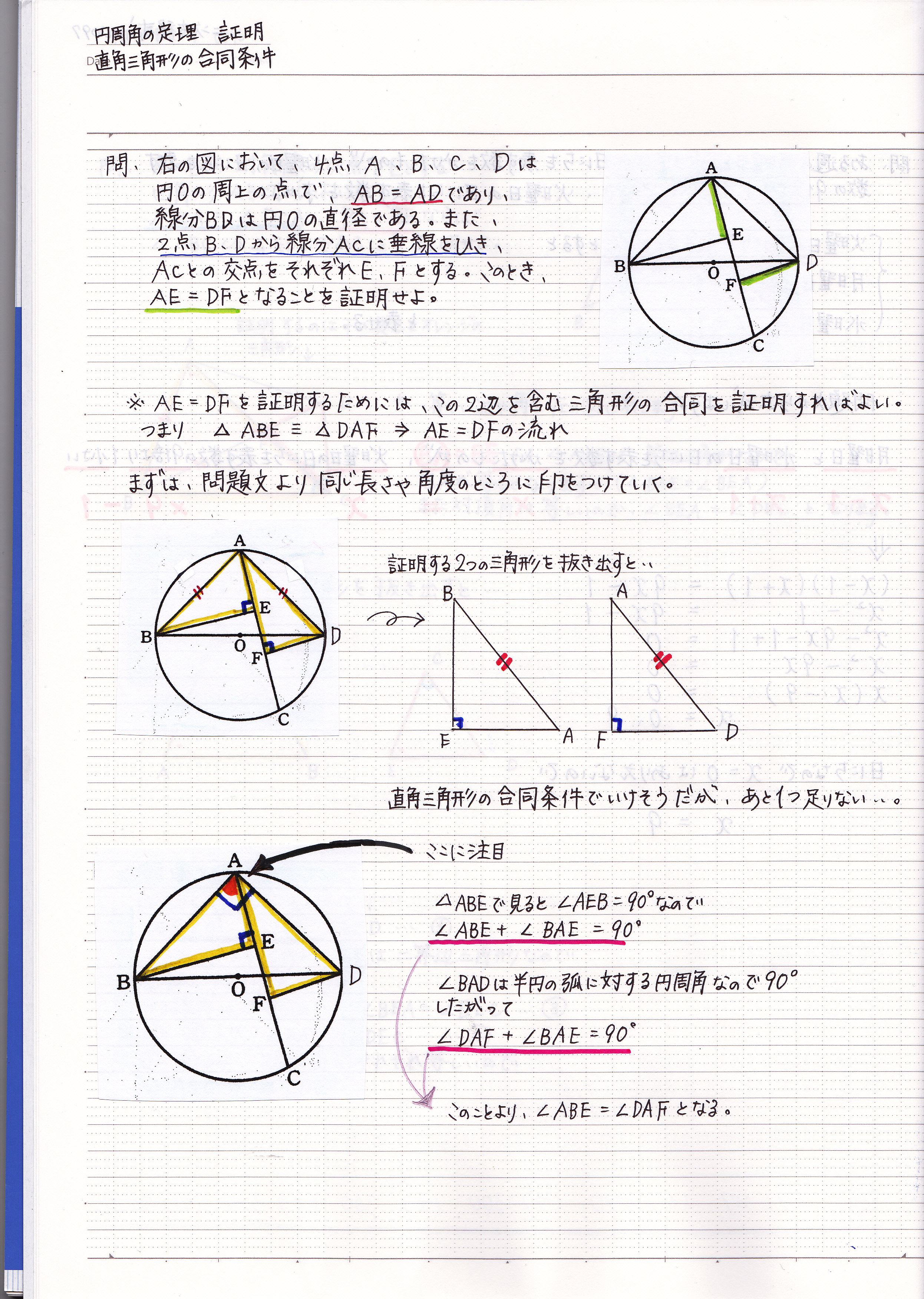



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方




学診 三角形 合同証明問題 二重まる学習塾のブログ




中学数学の図形合同の証明の問題です Clearnote



Mathematics 平行と合同 証明の書き方 2 よく出る問題 働きアリ




单位离职关系证明word模板 完美办公




File 最高人民法院关于银行储蓄卡密码被泄露导致存款被他人骗取引起的储蓄合同纠纷应否作为民事案件受理问题的批复 Pdf Wikimedia Commons




销售合同模板下载 销售合同违约金规定 Word模板网



方万律师事务所



Fidic合同条件下的不可抗力索赔 山东省对外投资与经济合作商会




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学




Sdrty5l9g8ngsm
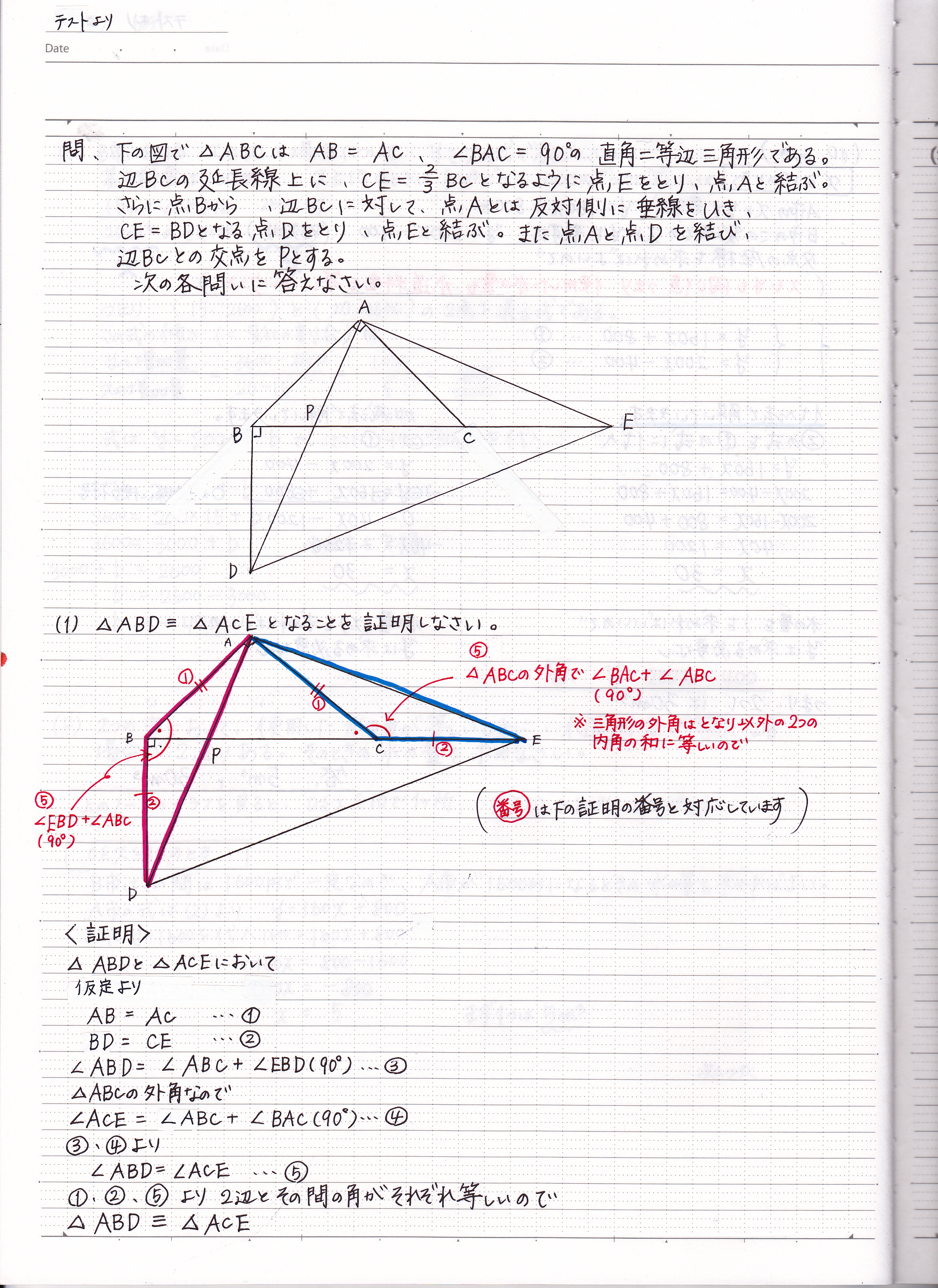



図形の総合問題の解き方 合同証明 三平方の定理 相似など 現役塾講師のわかりやすい中学数学の解き方




Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 合同の証明 働きアリ
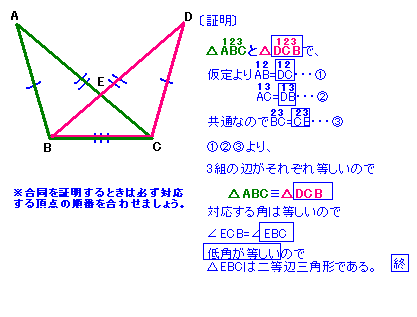



証明問題424 三角形の合同 中学数学の問題を解くコツ




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張




三角形の合同条件と証明問題の解き方 数学fun



头条问答 离职证明是否可以写 严重违反管理制度 不能胜任工作 等此类离职原因 为什么 赵胖说职场的回答 0赞



1



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



聘请 法律顾问 是企业最高效的投资 6大作用实力证明 上海明迈律师事务所 上海明迈律师事务所



1




又是掌门裁员出问题 员工 不签 自愿离职证明 就不发工资 陈某某



中2数学 通年用問題集 8章 合同の証明演習




没签劳动合同 怎么证明劳动关系 湛江市人民政府门户网站




合同协议书 合同协议模板 合同协议范文免费下载 超级合同



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
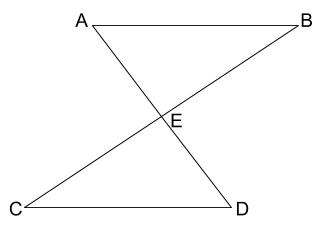



中学数学 三角形の合同の証明 その1 中学数学の無料オンライン学習サイトchu Su



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor




公司员工离职证明范本 公司协议 合同范文 优合同



没签劳动合同 怎么证明劳动关系 唐山人力资源网




中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su



证件证明类翻译需要注意很多细节问题 行业动态 驾照翻译 合同翻译 翻译机构 译博专业翻译公司
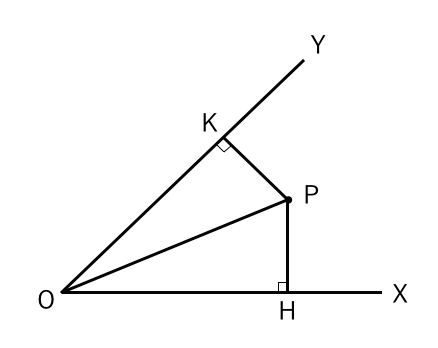



直角三角形の合同 証明問題 苦手な数学を簡単に
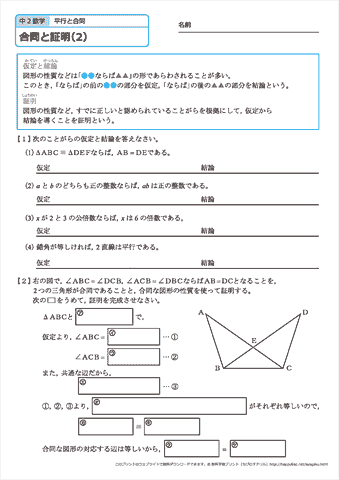



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




迪巴拉 我无需向任何人证明任何事 合同问题二月讨论 楠木轩
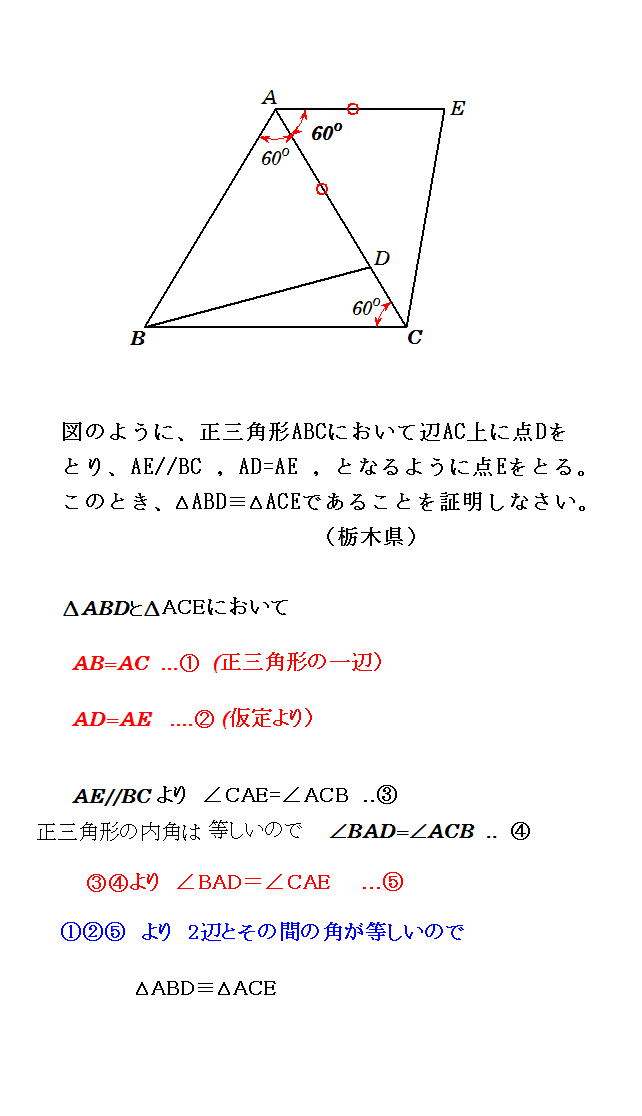



三角形の合同の証明問題の答え ネコネコ算数数学ページ




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学
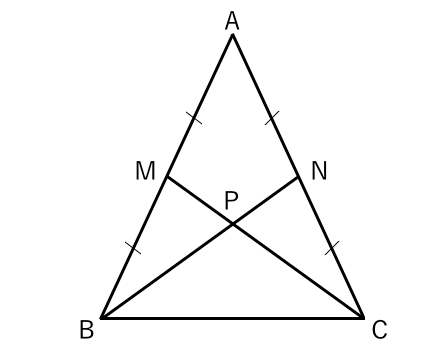



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step




三角形の合同証明の練習 無料で使える中学学習プリント



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 合同の証明 働きアリ




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



离职解除劳动合同证明书 离职解除劳动合同协议书下载范本 乐游网手机下载站



公司没有员工拒绝续订劳动合同的证据 要付经济补偿金




Manbet手机登入 Manbetx苹果客户端2 0 銷售合同涉稅條款的稅務籌劃全解析 Manbet手机登入 Manbetx苹果客户端2 0 Manbetx最新下载
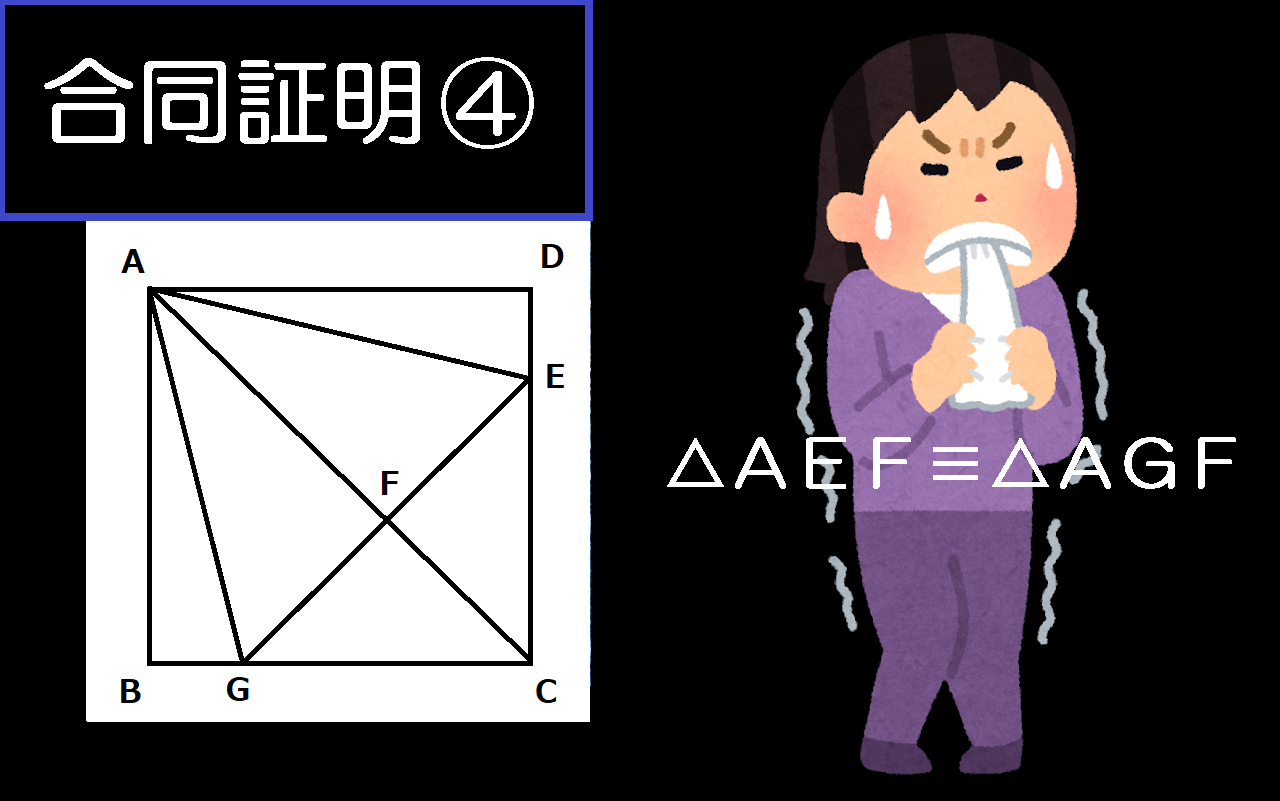



かんたん むずかしい 合同証明の記述問題をマスターしよう その4 栄南中 栄町中の生徒さんの挑戦を待っています 札幌自学塾新道東店




どの三角形の合同を証明すべきか 17年度北海道 高校入試 数学 良問 難問
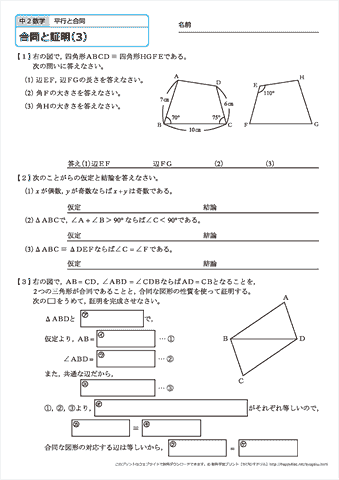



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
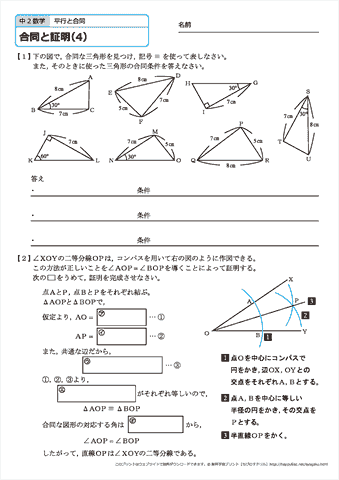



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



84 995澳门论坛资料大全 主頁欢迎您




世界一わかりやすい数学問題集中2 4章 平行と合同と証明
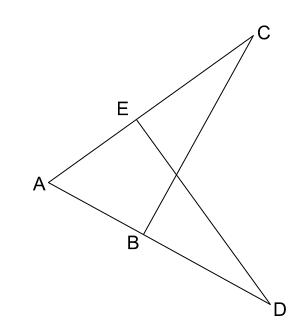



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su
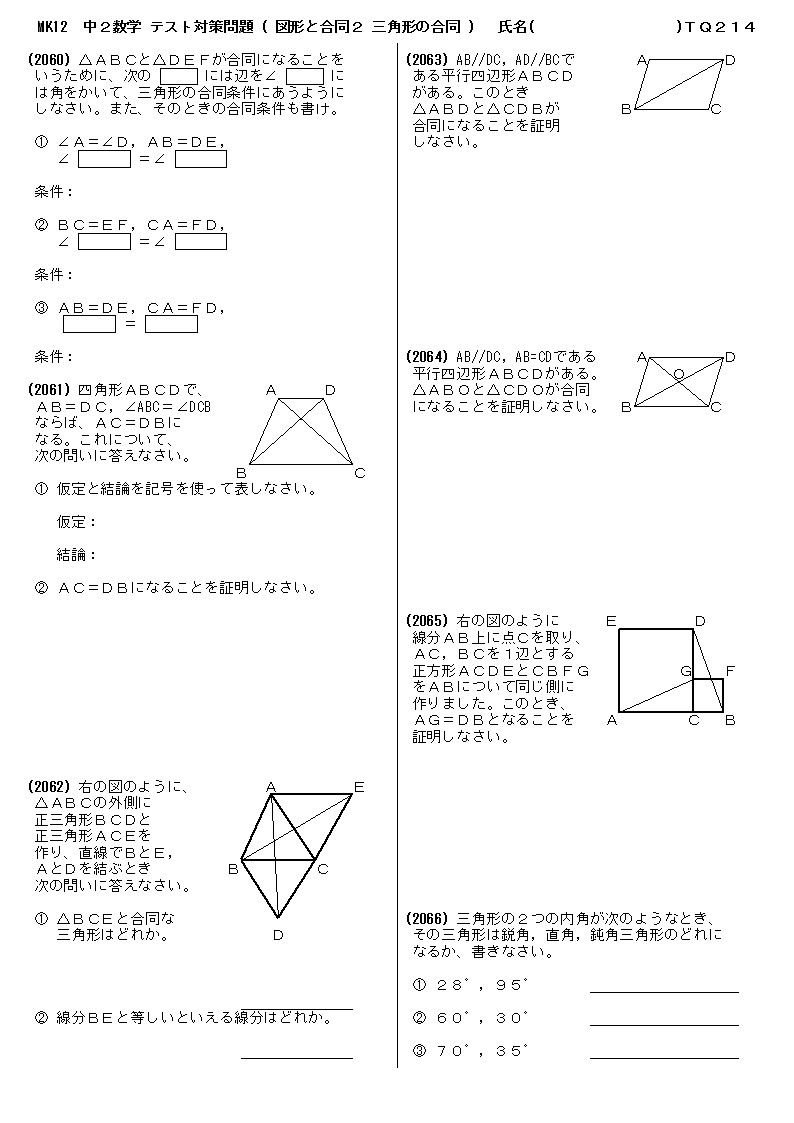



無料 中2数学 テスト対策 問題プリント 214 図形と合同2 三角形の合同



Google Adsense 纸质证明文件申请方法 泪雪博客




涨知识 上犹五家企业获得 守合同重信用 企业证明 江西省



断桥铝型材采购合同范本 Word版



订立劳动合同阶段 企业千万别陷入这7个大 专家顾问 河南瀛汉律师事务所



没签劳动合同怎么仲裁 河南锦盾律所法务部




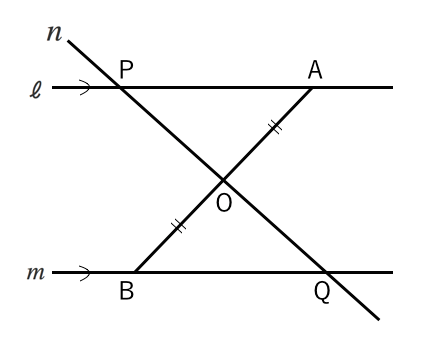
平成25年長野県立高校 入試問題 図形の証明問題 合同 現役塾講師のわかりやすい中学数学の解き方



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




中学 数学 実力テスト 過去問 1次関数 合同の証明 問題と解答 赤城 ᐡᐤᐡ



合同な図形 三角形の証明問題 苦手な数学を簡単に



2




合同协议书 合同协议模板 合同协议范文免费下载 超级合同




正三角形の合同証明 無料で使える中学学習プリント



生活常见法律问题 房屋租赁合同简析



疑似伪造合同 证明材料



个人收入证明你达标吗 不满足这几点 小心签了购房合同贷不下款 流水
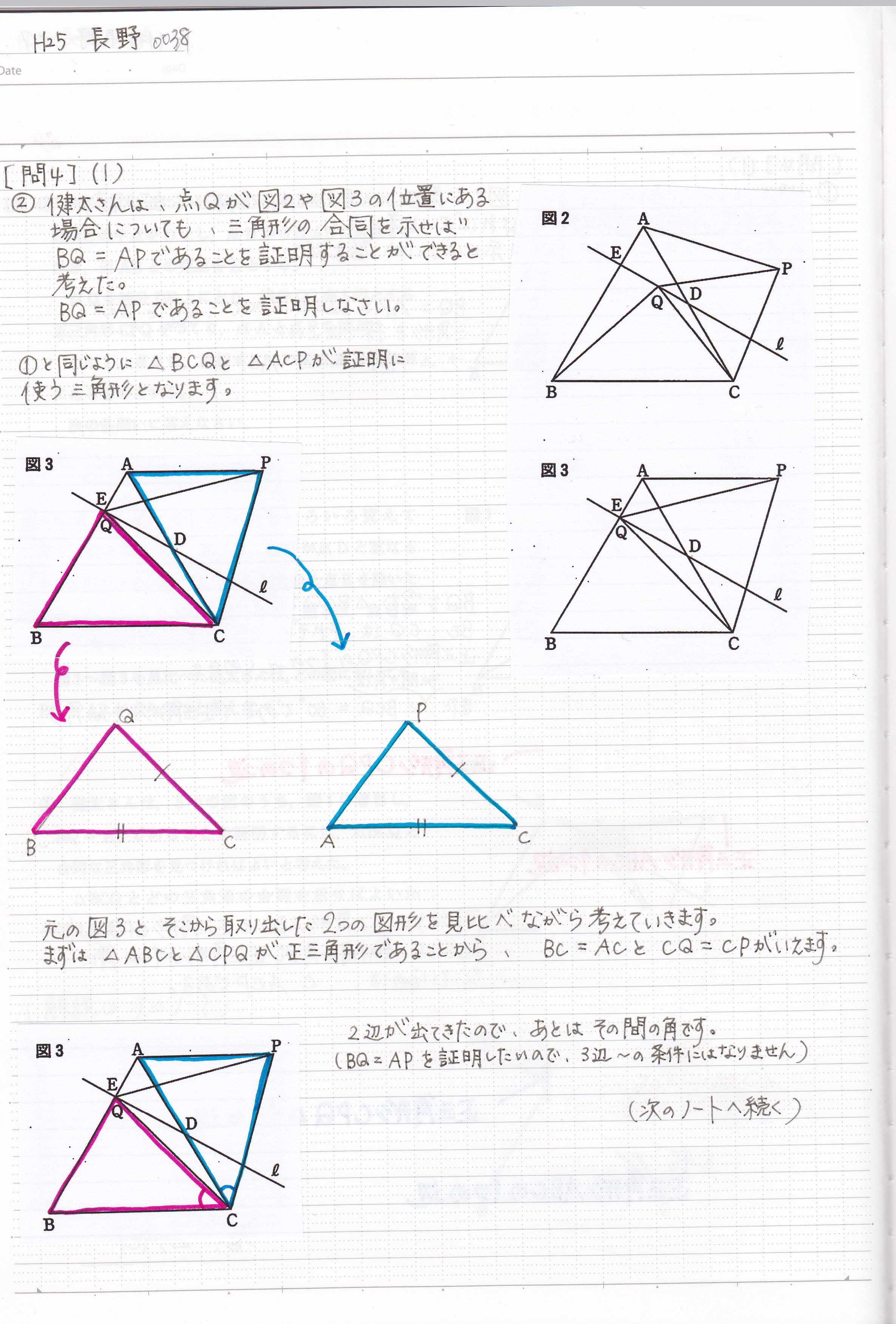



平成25年長野県立高校 入試問題 図形の証明問題 合同 現役塾講師のわかりやすい中学数学の解き方



18年龙华教师招聘报名问题 怎么证明工作证明 是用合同吗




File 最高人民法院关于审理技术合同纠纷案件适用法律若干问题的解释 Pdf Wikimedia Commons



头条问答 自己公司最近出了一项规定 如果员工自愿离职 公司不给开解除劳动合同证明 这合法吗 该怎么办 荷在职场的回答 0赞
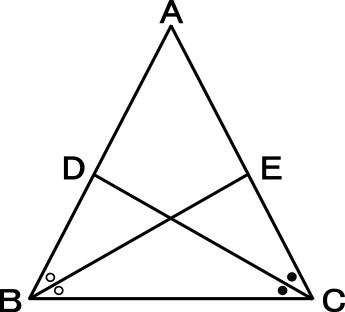



中学2年数学練習問題 図形と合同 三角形の合同の証明問題
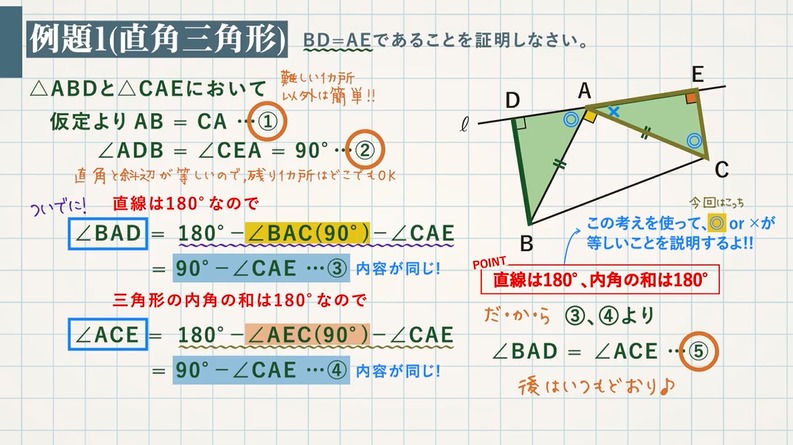



考え方はまったく同じ 合同 相似の証明でよく出る応用問題 教遊者
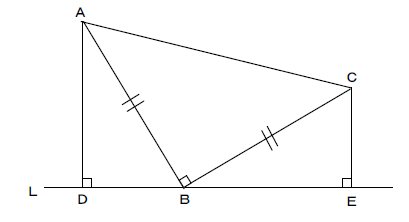



中2数学 直角三角形の合同条件を使った証明の定期テスト過去問分析問題 ダイスト



0 件のコメント:
コメントを投稿