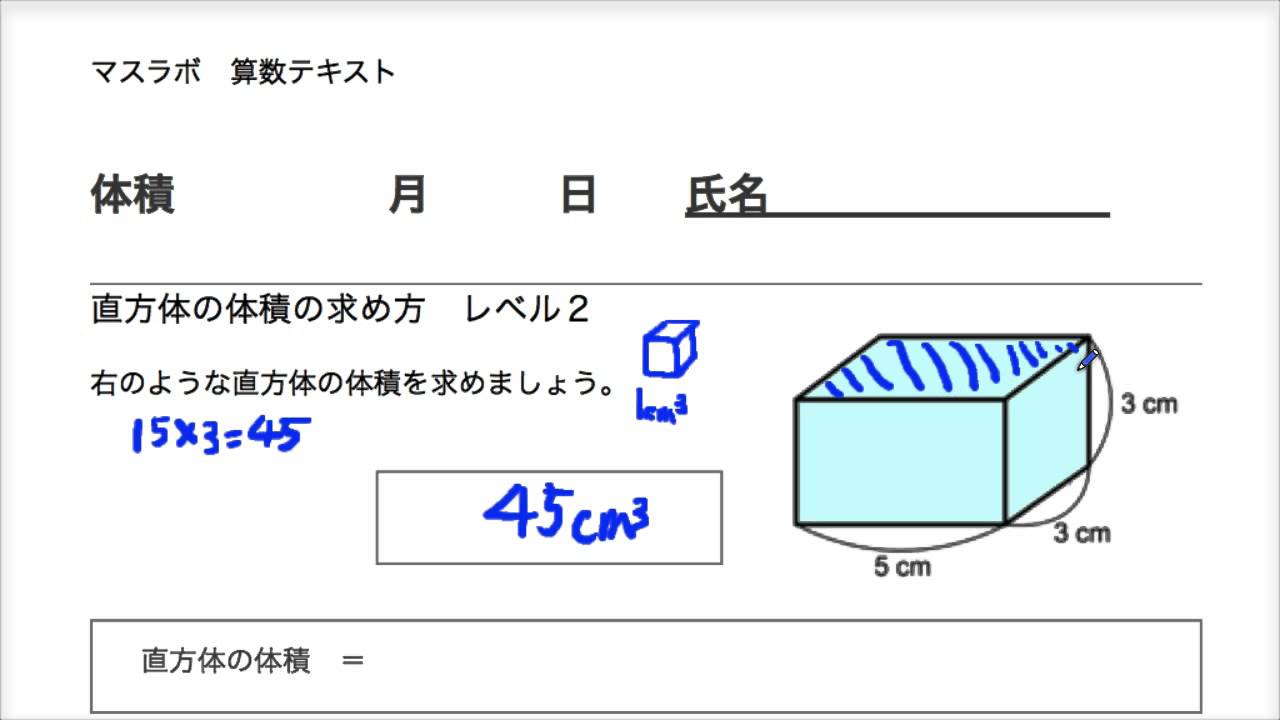
基本的に立方体や直方体のような6面体の場合には1面の面積を計算して合算するという方法で表面積を求めることが出来ます。 それぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 (c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 (c m 3) 円錐の体積・表面積の求め方(公式)について、図で解説しています。画像をスマホに保存立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答 すい体の体積=底面積×高さ×1/3 表面積は展開図から考えましょう。 円すいの表面積の求め方 円すいの側面積と表面積の求め方をしっかり学習してください。 →おうぎ形の円周、面積の求め方も確認しましょう。 例)下のような円すいの表面積を求めます。
直方体の表面積と立方体の表面積の求め方を教えて下さい 直 Yahoo 知恵袋
表面積の求め方 直方体
表面積の求め方 直方体-立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)0 回答 ベストアンサー カナヲ推しの小6🍒🌸。ʚɞ 。💌 約1年前 3種類の長方形の面積をそれぞれ求めて、2倍する! 0 ♡みみ♡ 約1年前 ありがとうございます🙌💕 0 この回答にコメントする 回答 Mayu🦋 約1年前 (縦×横+横×高さ+高さ×



直方体の表面積と立方体の表面積の求め方を教えて下さい 直 Yahoo 知恵袋
第41回直方体と立方体(体積と表面積)①の授業プリント&授業映像 更新日: 年9月6日 第41回直方体と立方体(体積と表面積)①の授業プリントはこちらから印刷できます。 → 第41回直方体と立方体(体積と表面積)①(問題) 第41回直方体と立方体立方体・直方体の体積の求め方|小学生に教えるための分かりやすい解説 管理人 9月 , 18 / 12月 1, 18 立体図形は平面図形の延長線上にある単元ですが、立方体・直方体は立体図形の初めに習う最も基礎的な概念に当たります。立体の体積という新しい分野なだけに、なかなかイメージしVolume = length * width * height;
直方体の体積の求め方 https//youtube/Jy71xBjf4直方体の表面積の求め方 https//youtube/tzGq3e9V15k体積・表面積の求め方〈中級①〉 https//youtube/Sk0dppi9kH03 下の図の①~③の投影図は直方体 円・おうぎ形の面積 おうぎ形の面積の求め方 A 弧AB B 中心角 O 半径 360° 円の面積 = 半径 × 半径 ×π 円周 = 直径 ×π ① おうぎ形の面積 = 円の面積 × 中心角 360° ② おうぎ形の面積 = 円の面積 × 弧 AB の長さ 円周の長さ 1 半径 3 cm の円と与えられた中心角の右の(1)は直方体に円柱をさしこんだ もので、(2)は立方体に1辺8cmの 正方形を底面とする直方体で反対 側の面までくりぬいたものです。 それぞれの立体の体積と表面積を 求めなさい。
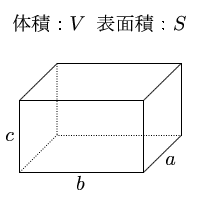
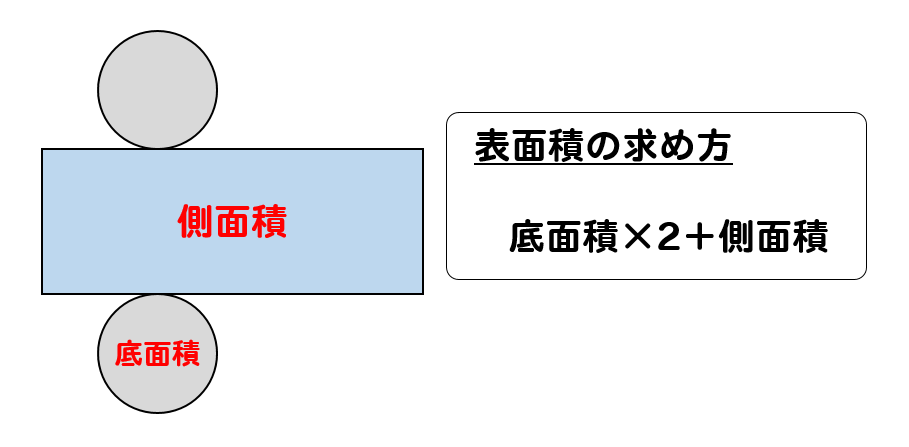
中学1学年 柱体、錐体、球の表面積と体積 ②単元観 本単元は、角柱や円柱の体積を、直方体や立方体の体積の求め方をもとにして、これらの立体の体 積も計算によって求められることを理解したり、体積の求め方を説明したりできることをねらいとす る。} いくつかの実行結果です。 直方体の縦・横・高さを入力 縦 = 2 横 = 4 高さ = 5 直方体の体積 V = 直方体の表面積 S = 以下の図のような四角柱(直方体)の表面積を求めます。 求め方としてはまず四角柱(直方体)の 展開図を考えることがポイント です。 以下の図の赤色が底面、青色が側面です。 赤い部分の面積、つまり 底面の面積 を底面積、青い部分の面積、つまり 側面の面積 を側面積といいます。 この 底面積と側面積とを合わせたもの が表面積となります。




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




立体の体積を求める公式
求める表面積は,小さい円柱の側面積と大きい円柱の表面積の和 に等しいから, 3× 2π×1 3× 2π×2 π×2 ×2=26π (cm2) 159 次の立体は,直方体,立方体,円柱が組み合わさった立体である。体積と表面積⑵ この直方体の表面積を求めなさい。 体積・表面積⑴ 立方体・直方体 8 ステップ3 複合図形の体積 7 図の立体は、直方体を組み合わせてできた立体です。この立体の体積 を3通りの求め方で求めようと思います。 ⑴ 下の図のように、この立体を上下に2つに分割しました。 ① 上の立体の体積47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。




公式を図解 すい体の体積 円すいの表面積の求め方




表面積の求め方 計算公式一覧
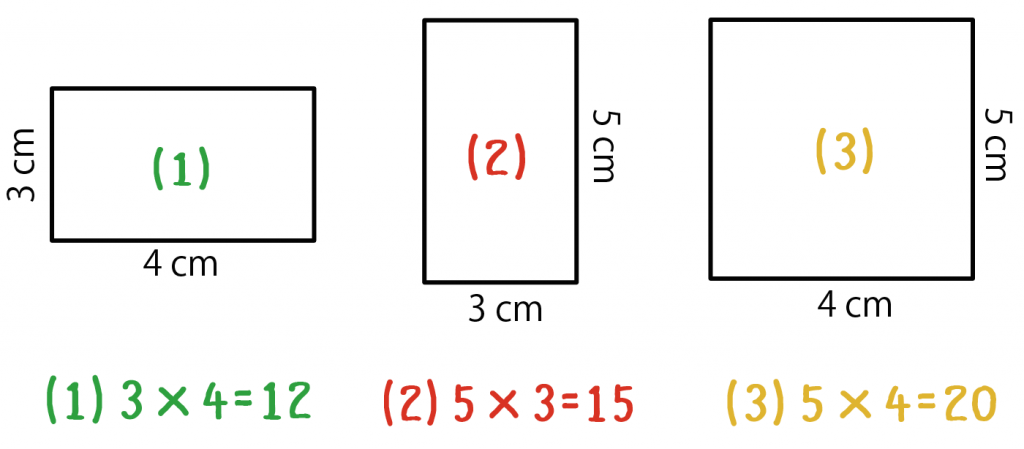
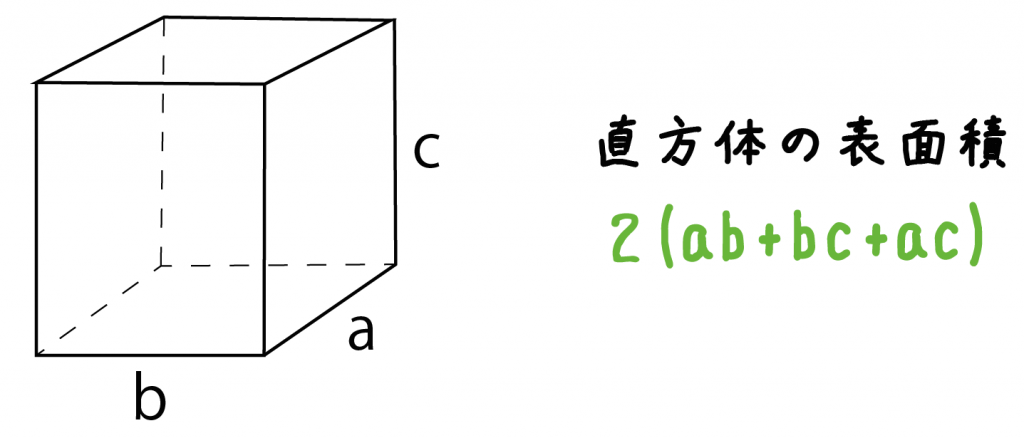
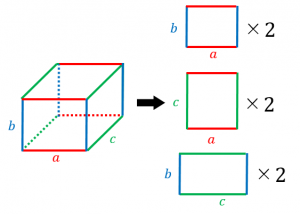
Printf("直方体の表面積 S = %3f\n", surface); 表面積を求めるときには、底面の面積である「底面積」と側面の面積である「側面積」をそれぞれ計算して足し合わせるのが一般的です。 つまり「底面積+側面積=表面積」が基本といえます。 ただし三角形・四角形・円など底面の形が違っている点にまず注意しなければなりません。 さらに立体にしたときに柱や棒のように太さが一定の「柱体」のとき直方体の表面積の求め方は? 1分でわかる計算、公式と例題 よって、異なる3つの長方形の面積(縦の長さ×横の長さ)の合計を2倍すれば「直方体の表面積」となります。 直方体2本の体積は 4×4×12×2 =384cm 3 。 重なっている体積は 4×4×2=32cm 3 。 求める



直方体の表面積 簡単に計算できる電卓サイト



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
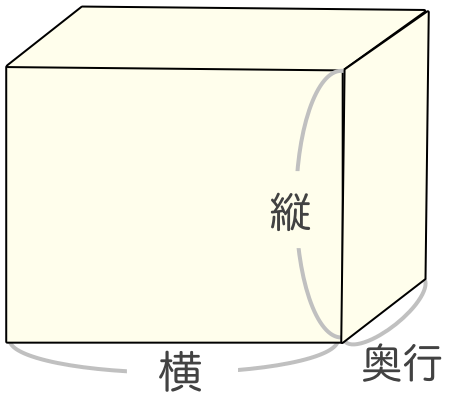
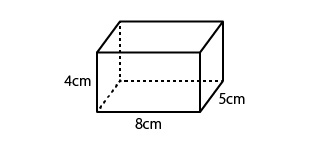
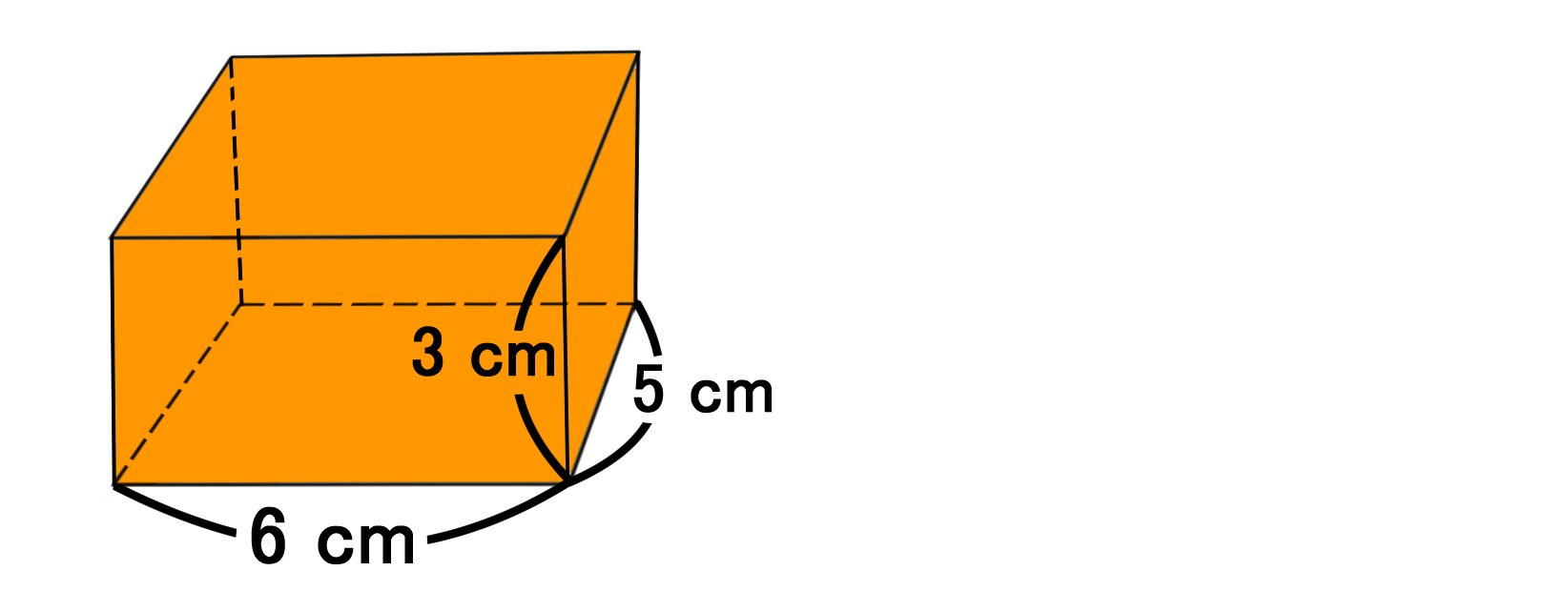
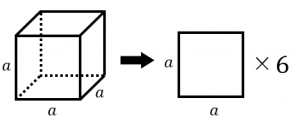
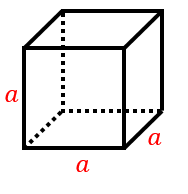
表面積 S = 6 a 2下図の直方体の表面積と体積を計算してください。 a=2cm、b=4cm、c=5cm です。あとは前述した式に代入すればよいです。 直方体の体積は「縦×横×高さ」で求めます。よって、 となります。 まとめ 今回は直方体の表面積の求め方について説明しました。直方体の表面積Sは、S=2ab2bc2acで計算します。直方体は6面の長方形で構成される立体図形です。また、向かい合う面 立方体の六つの面は全て等しいので、立方体の表面積は、一面の面積を求めて6倍すれば求められます。以下の手順に従って、立方体の表面積を求めましょう。 立方体の表面積は、六つの面の面積からなります。立方体の全ての面は等しいので、一面の面積を求めてそれを6倍すれば、表面積の合計が分かります。表面積は簡単な公式6 x s2で求められます。「s 」は立方



直方体を組み合わせた立方体の面積 写真参照 を解きたいのですが Yahoo 知恵袋




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学
/* 直方体の表面積の計算・出力 */ surface = 2 * (length * width width * height height * length);三辺の長さが $a, b, h$ の直方体の表面積 $S$ は、次の式で求められます。 直方体の表面積 \begin{align*} V = 2(abahbh) \end{align*} 表面積 = 2 × (たて × 横 + たて × 高さ よこ × 高さ)Printf("直方体の体積 V = %3f\n", volume);




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球の体積計算
展開図(直方体・立方体):重なる点・平行な辺と面 積み重ねられた立体①:表面積と体積! 投影図→見取り図のテクニック2つ!(積み重ねられた立体②) 積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③) くり抜かれた立方体は「重なり」体重あたり、つまり体積あたりの表面積は 立方体の積み木を四つ積んで大きい立方体を 作ると体積あたりの表面積が半分になることで 直感的に説明できます。6年 算数 学研教育情報資料センター 学習相談 小/算数/6年/量と測定/ 立体の体積と表面積/理解シート



Q Tbn And9gctjav6gvj1k5jlr5jeyhgdtl 5v264jxhqxszqv9lgkyrvbr9tp Usqp Cau




表面積の求め方 計算公式一覧
直方体の表面積から1辺の長さ・体積を公式を使って計算します。 縦・横・表面積を入力し「直方体の1辺・体積を計算」ボタンをクリックすると、直方体の高さ・体積を計算して表示します。 縦の長さ a: 横の長さ b: 表面積 S: 縦の長さaが3、横の長さbが4、表面積Sが94の直方体の高さ・体積この直方体を頂点a,c,fを通る平面で分けたときにできる三角 錐 すい bafcの表面積を求めなさい。 (17年秋田県立高校入試問題) (cm 2 ) 図1のような直方体を上下はそのままで4個はり合わせて、 図2のような立体を作ります。 図1の直方体4個分の表面積の和と図2の立体の表面積の比は 5:4となりました。 図1 図2 (1)「あ」の長さは何cmですか。




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円柱の表面積の求め方 公式 小学生 中学生の勉強
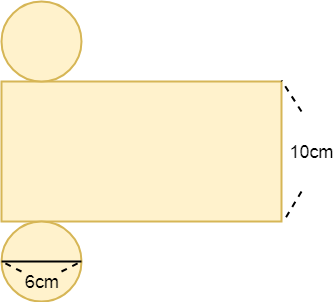
2.直方体の体積の求め方 直方体がどのような形をしているのか解かったところで、次は直方体の体積を求めてみましょう。 体積とは、図形の中の空間や数量を表したもので、縦×横×高さで求めることができます。 下の直方体の図形を使って説明します。 円柱の表面積の求め方公式 円柱の表面積を求めるときには次の公式を使います。 円柱の表面積=底面積×2+円柱の側面積 円柱の側面積 =円柱の高さ×底面の円周の長さ なので 円柱の表面積=底面積×2+円柱の高さ×底面の円周の長さ とも書けます。直方体と立方体の体積・表面積! 中学受験算数体積表面積ゼロから始める中学受験算数46 スッキリ解決! 直方体と立方体




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
よって,この直方体の表面積は,(24+48+72)×2=2 なる求め方の方が,簡単です。 直方体全体の体積は,12×17×9=16 (㎝3) です。 板の厚さは1㎝ですから,くりぬく部分の たての長さは,12-1×2=10(㎝)です。 横の長さは,17-1×2=15(㎝)です。 (次のページへ) 9cm 17cm 12cm 9cm 17cm 直方体の体積の求め方には公式があるんだ。 直方体のタテの長さをa、ヨコの長さをb、高さをcとしよう。 このとき直方体の体積は、 abc で計算できちゃうんだ。 つまり、 タテ×ヨコ×高さ ってことだね。 今日は公式をマスターするために、例題を一緒にといてみよう! 直方体の体積の求め方 数学・算数 表面積一定の直方体の体積の考え方 表面積一定の直方体の体積が最大にとなる 条件について考えてます。 横をx 縦をy 高さをz とおくときx=y=zとなることは直感でわかるのですが これ 質問No



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方



直方体の計算 もう一度やり直しの算数 数学
回転体の表面積も求めよう! では次,曲線をx 軸やy 軸のまわりに回転してできる回転体の曲面の表 面積を求める公式についても解説しておこう。 (Ⅰ) について,微小区間x, +Δ における 微小な曲面の表面積 ΔS は,図12 より



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




表面積の求め方 計算公式一覧



立方体と直方体の表面積を計算する 具体例で学ぶ数学



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式



1




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




四角錐の表面積の求め方 公式 小学生 中学生の勉強




表面積の求め方 計算公式一覧




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




小5 算数 小5 5 体積の求め方のくふう Youtube




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




表面積の求め方 計算公式一覧




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




角柱の表面積 Youtube



直方体の体積 表面積 体積 表面積の計算 計算サイト



三角錐の表面積側面積底面積の求め方 公式 写真の形の名前 Yahoo 知恵袋




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円柱の体積の求め方 公式 小学生 中学生の勉強




四角錐の表面積の求め方 公式 小学生 中学生の勉強



直方体の表面積の求め方は 1分でわかる計算 公式と例題




中1数学 立体の表面積 について 空間図形 ひっそりと物理や数学を解説する




円柱




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu



1




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
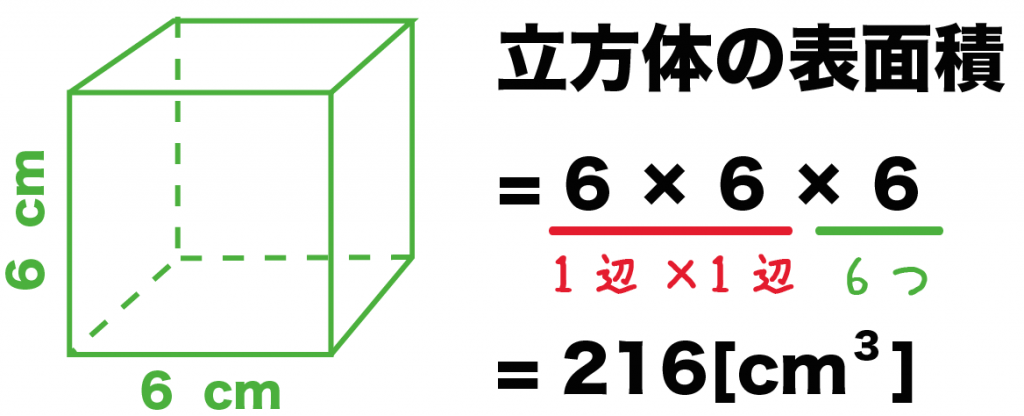



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




表面積の求め方 計算公式一覧
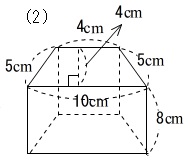



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



1




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




円柱の表面積 Youtube



5 5 複雑な立体の表面積と面積を求めるには さんすうがく




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座
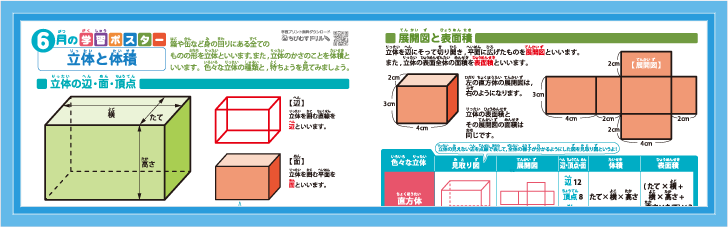



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



直方体の表面積と立方体の表面積の求め方を教えて下さい 直 Yahoo 知恵袋



立方体と直方体の表面積を計算する 具体例で学ぶ数学



球の体積 面積を求める公式を教えてください 出来れば中学生でも理 Yahoo 知恵袋



立方体と直方体の表面積を計算する 具体例で学ぶ数学




直方体の表面積の求め方 Youtube




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




円柱の表面積と体積を求める公式 具体例で学ぶ数学




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 立方体 長方体 小学生 算数のノート Clear




体積 表面積




円柱の表面積の求め方 公式と計算例




公式を図解 すい体の体積 円すいの表面積の求め方




5月8日 小5 算数授業動画 中学受験塾act アクト のブログ
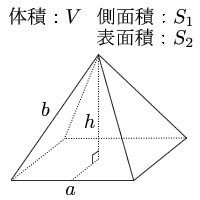



正四角錐 底辺と高さ 体積 表面積の計算 計算サイト
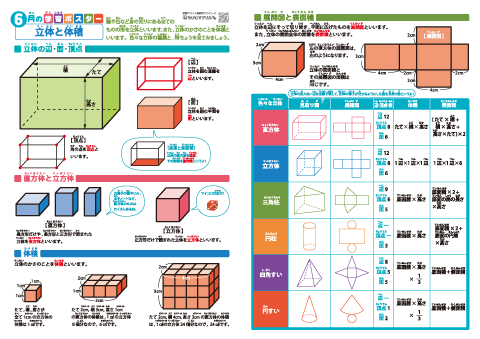



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




公式を図解 すい体の体積 円すいの表面積の求め方




角柱の体積 Youtube



表面積のすべて 苦手な数学を簡単に




Hd限定円錐 体積 の 求め 方 ページを着色するだけ



直方体の表面積の求め方は 1分でわかる計算 公式と例題
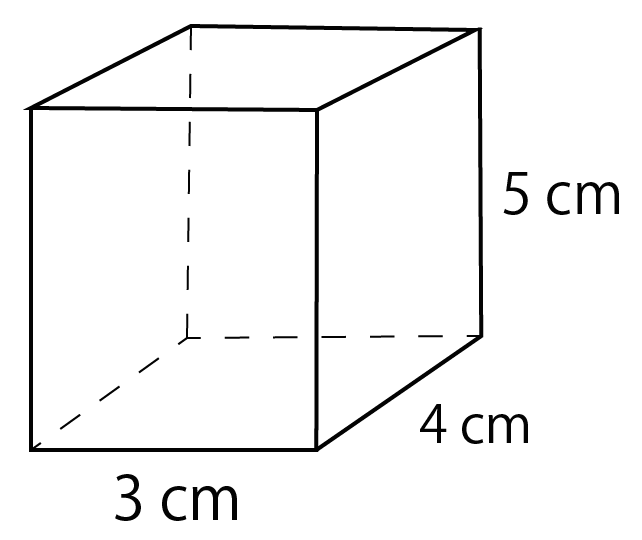



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




小5 算数 小5 3 直方体と立方体の体積 Youtube




円柱の表面積と体積を求める公式 具体例で学ぶ数学




図形の問題です 4 の求め方が考えても分かりません Clear




公式を図解 すい体の体積 円すいの表面積の求め方
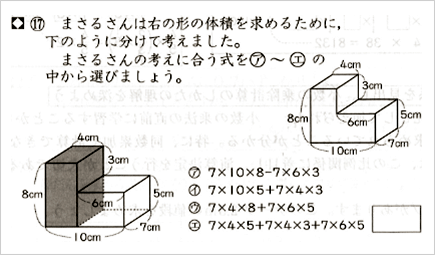



直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館
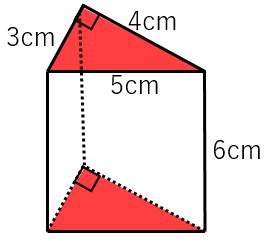



三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




円柱の表面積の求め方 公式 小学生 中学生の勉強




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿