このように自然数を素数の積に分解することを素因数分解という。 素因数分解の考え方 素数になるまで、小さい素数で順にわっていく。 2)12 ←素数2 で割る 2) 6 ←素数2 で割る 3 ←素数 基本問題 次の数を素因数分解しなさい。最大公約数と最小公倍数 素因数分解 一次方程式の解 二次方程式の解 三次方程式の解 四次方程式の解 一次不等式の解 二次不等式の解 三次不等式の解 四次不等式の解 二元連立方程式 n次方程式の解共通の約数(=公約数) 1 , 2 , 3 , 6 の中で最大のものは 6 ⇒ 最大公約数は 6 間違って「最小公約数」などと言わないように.最小公約数は,計算しなくても1に決まっているので「最小公約数」などという用語は使わない.(=当たり前でつまらないことだから)
素因数分解のドリル
素因数分解 最大公約数 問題
素因数分解 最大公約数 問題-最大公約数を求める計算機 留意事項 最大公約数 (GCD)を簡単に求める計算プログラムです エクセルじゃないですが、最大5つの数に対して計算可能です 入力値は最大5桁までの整数に限ります(負荷の関係で適当に制限かけてます) 入力値が「0」の場合は最大 公約数 問題 難しい by 鳩 雛 鳴き声 鳩 雛 鳴き声




公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun
「1」×「その数自身」でしか表せない「数」があります このような数のことを「素数(そすう)」といいます 次に素因数分解とは「自然数」を「素数」だけの積の形( × )で表すことです この「素因数分解」を使う問題を一緒に見ていきましょう この年齢になって、ちょっと恥ずかしいのですが素因数分解について質問があります。なぜ素因数分解で「最小公倍数」や「最大公約数」がわかるのでしょうか?最大公約数の場合、例えば8と12だと 2)8 12 ーーーーーー 2)4 素因数分解と公約数・公倍数をマスターすれば、分数の約分・通分は楽勝です。 分数を暗算でガンガン解くことができます。 公約数と公倍数の学習マニュアルはこんな感じ。 最大公約数ドリル ①小さな数で大きな数を割る 4:12 12÷4=3 割り切れるので4
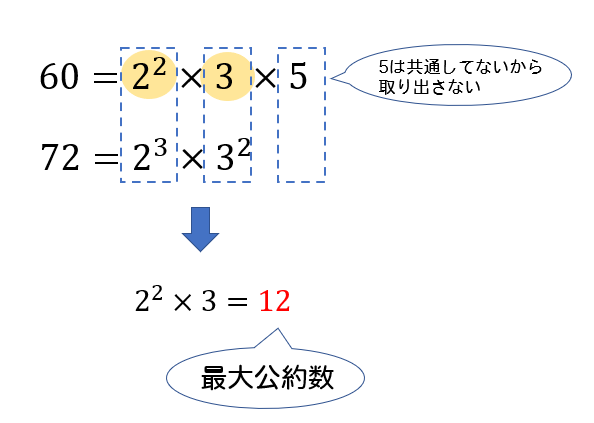
詳細な解法を提供する Microsoft の無料の数学ソルバーを使用して最大公約数について学習しましょう。 素因数分解 次に類似した 5 個の問題 gcf(12,16) g c f (1 2, 1 6) 次に類似した 5 個の問題 gcf(3,4) g c f (3, 4) 中学までに筆算での求め方を習ったかもしれないが,\ 応用性に欠ける \\2zh 高校数学では,\ \bm{素因数分解}して求めるのが基本となる \\1zh \bm{最大公約数は,\ 共通する素因数をすべて取り出して掛ける}と得られる \\2zh (1)\ \ 2を2個と3を1個取り出せば約数の個数と素因数分解1 ・270を素因数分解しなさい。 ・素因数分解を利用して,次の整数の約数の個数をそれぞれ求めなさい。(32 72 126) 約数の個数と素因数分解2 ・1から30までの整数のうち,約数が4個である整数は全部で何個ありますか。 素因数分解の応用1 (1)
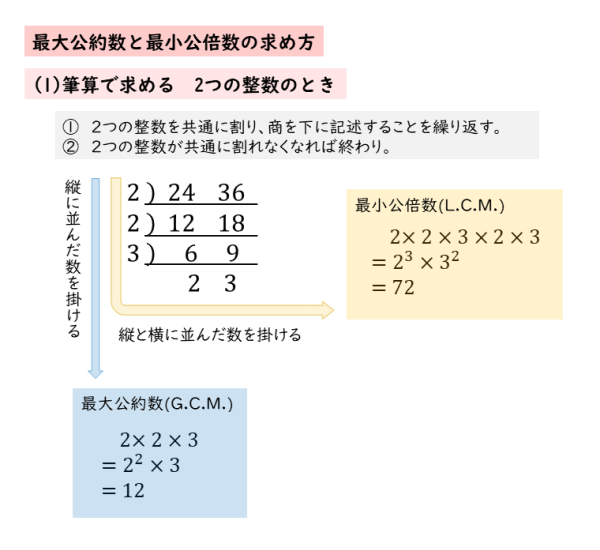
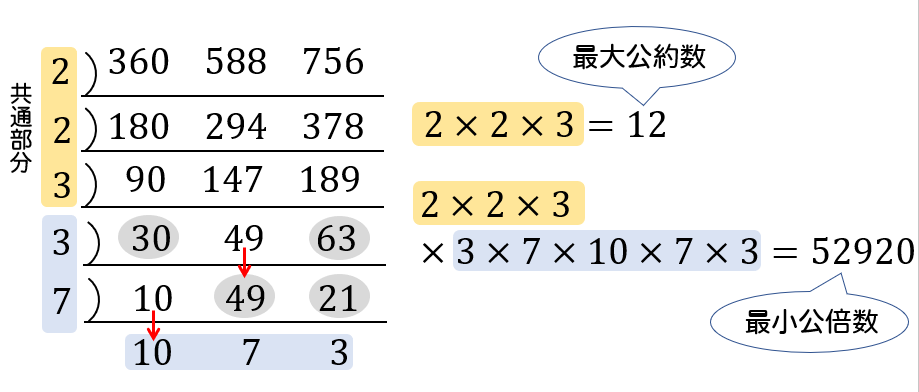
素因数分解を活用して、これらの最大公約数、最小公倍数を求めてみましょう。 (1)\(60, \ 72\) をそれぞれ素因数分解をします。 最大公約数とは、それぞれの共通する素因数をすべて取り出して掛け合わせた数。2数の最大公約数と最小公倍数の求め方 例)1と144 ① それぞれ素因数分解する。 ② 素因数分解の結果を利用して,最大公約数と最小公倍数を求める。 2)1 2) 60 2) 30 3) 15 5 2)144 2) 72 2) 36 2) 18 3) 9 3 1=2*2*2 *3 *5 144=2*2*2*2*3*3 左に並んでいるのが12と18と30に共通する素因数なので、その積が最大公約数,左と下に並んでいるのが全種類の素因数なので、その積が最小公倍数になります。 答 最大公約数 6, 最小公倍数 180 さっきやった素因数分解式の図はこうでした。




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学
素因数分解でもいいことはありますよ。 24 = 2^3 x 3^1 90 = 2^1 x 3^2 x 5^1 最大公約数は次数の小さい方の素因数を掛け合わせればよいので 2^1 x 3^1 = 6 最小公倍数は次数の大きい方の素因数を掛け合わせればよいので 2^3 x 3^2 x 5^1 = 360 共通の因数とかは考えず※ 素因数分解の結果が分かる次のような2数を用いて,ユークリッド互除法による最大公約数,最小公倍数の計算結果を確かめることができる. 例 1763=41 × 43 , 1927=41 × 47 → g=41 例 =1013 × 151 , 7049=1013 × 773 → g=1013 例 =53 2 × 13 3, =53 × 13 4素数と素因数分解を活用した問 題解決の過程をふり返って検討 しようとしている。 ② 素因数分解の活用 ・素因数分解を利用した自然数の約数の求め方を考えること ・素因数分解を利用した2つの自然数の最大公約数の求め方を考えること (1) 素因数分解を



48s96ub7b0z5f Net Yukuriddo Gojoho Kihon



因数分解での共通因数と二乗数の見つけ方
前半(最大公約数・最小公倍数問題)解答・解説 方針1素因数分解もどきの利用 限られた時間のなかで効率よく解くには、素因数に完全に分解しないほうがおそらく簡単です。 解2.最大公約数の計算1 それでは、40と30の最大公約数を求めてみましょう。 まず初めに行う作業は、40と30をそれぞれ素因数分解します。 素因数分解とは、ある数を素数の積で表した形のことをい中3 素数·素因数分解 最大公約数·最小公倍数(2) 問題7、問題8、問題9、問題10のhelp 間違っている =>作者: 連絡ありがとう.めったにない変わったエラーでした・・・指数(肩に付ける小さい数字)が地上に降りていましたので訂正しました.
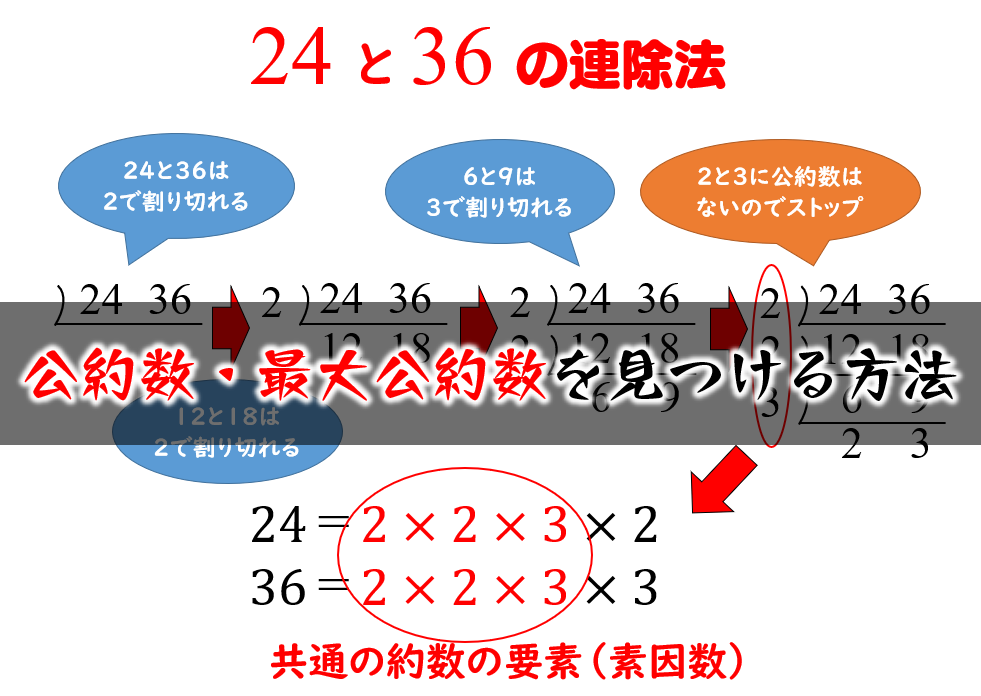



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




問題 素因数分解と公約数の基本 中学数学 理科 寺子屋塾の復習サイト
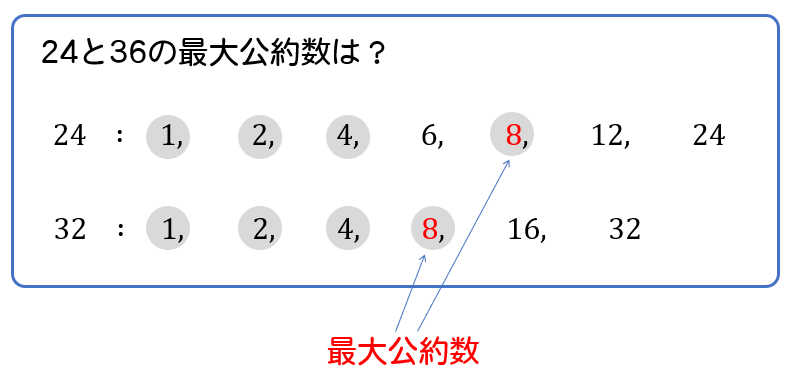
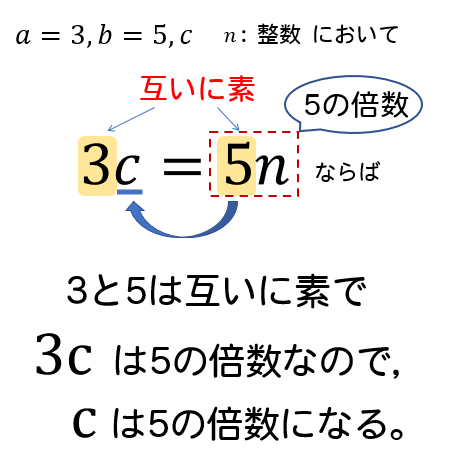
最大公約数でくくりましょう 最大公約数Gが15 上記のαとβは互いに素出ないといけない 互いに素なので、最大公約数以外で、225の素数である3と5をnの素数としてはいけない。 答え n=2×7×15=210 問題4 全て素因数分解を行う 最大公約数の5でくくる 「最大公約数って何?」と聞かれてあなたは何と答えますか? 最大公約数とは何かという質問に答えられないと、数学の問題では多々苦労する場面があります。 しかし、最大公約数にはそれだけじゃない、大学入試に役立つ性質がたくさんあります。 今回は最大公約数について、その定問題 次の2つの数の最大公約数を求めましょう。 最大公約数を求める時は、すだれ算を使って素因数分解して求めてください。 問1. 4と10 問2. 9と24 問3. 12と39 問4. と50 問5. 60と64 問6. 27と81 問7. 30と90
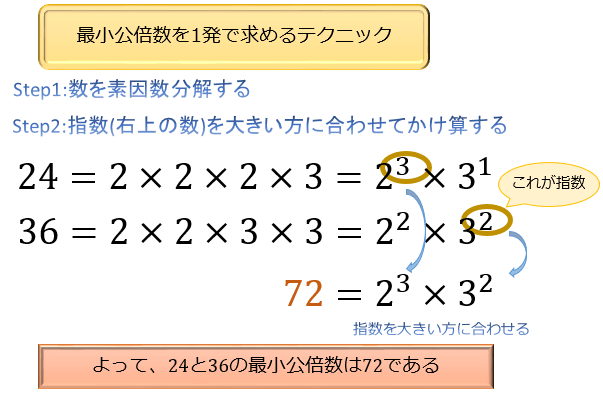



最小公倍数って何 その求め方と素因数分解のテクニック アタリマエ



ドリルズ 小学5年生 算数 の無料学習プリント小学5年生 最大公約数と最少公倍数
まず,最大公約数を次のいずれかの方法で求める. i 共通に割れるだけ割っていく方法 ii 素因数分解を利用して共通な指数を探す方法 iii ユークリッド互除法による方法 iiiでは最小公倍数を求める方法も示されるが,iiiのように最大公約数だけが求まるときは,右の関係式を用いて AtCoder の整数問題は、500 点以下であれば「 素因数分解 」と「 最大公約数 」と「 エラトステネスの篩 」と「 合同式 」に関する考察・アルゴリズムを自在に操れば、ほとんど解けるようになっています 2 。最大公約数の求め方と問題 最大公約数の求め方は3つありますが、そのうち下記の2つを紹介します。 ① 割り切れなくなるまで同じ数で割る ② 素因数分解した素数で、指数の最も大きな値 それぞれ解説します。 ① 割り切れなくなるまで同じ数で割る
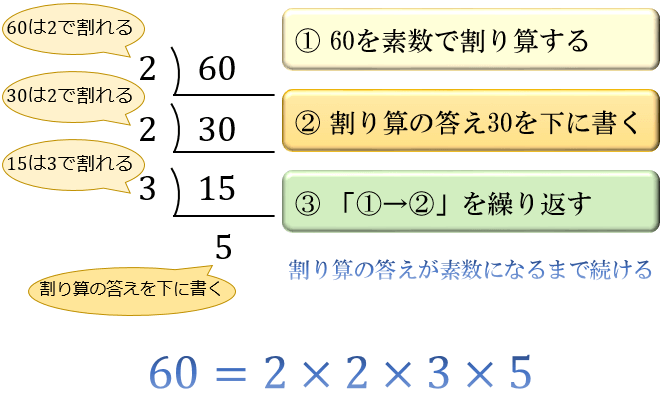



素因数分解のやり方 5つのステップで分かる素因数分解問題の解き方とコツ アタリマエ



最小公倍数の求め方や性質を全て解説 実際の入試問題の解説付き Studyplus スタディプラス
素因数分解の練習です。素因数として、2,3,5,7が考えられるような数が並ぶので、すだれ算などを駆使して、素数の積の形にしてください。 中学受験では必須の内容です。約分や割り算の計算練習としても優れています。 経過 09年10月23日 素因数分解1そこで、最大公約数の探し方のコツをおさえておこう。 ある2つの数(3つ以上の数)の最大公約数を求めるときには、まず、それらの数を 素因数分解 しよう。 でてきた素因数を見比べて、 指数が小さい方を選んでかけ算する と最大公約数になるんだ。 最大公約数 g g g を素因数分解したときの p i p_i p i の指数は min (e i, f i) \min(e_i,f_i) min (e i , f i ) 最小公倍数 l l l を素因数分解したときの p i p_i p i の指数は max (e i, f




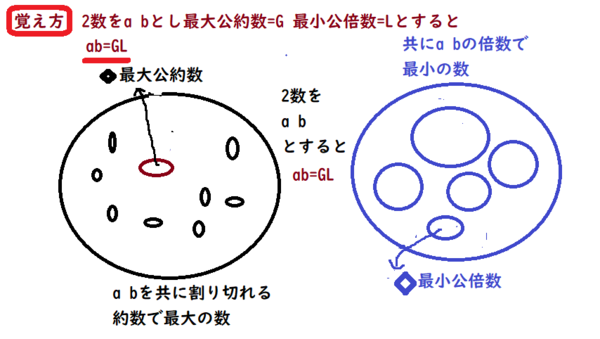
最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場



問題 素因数分解と公約数の基本 中学数学 理科 寺子屋塾の復習サイト
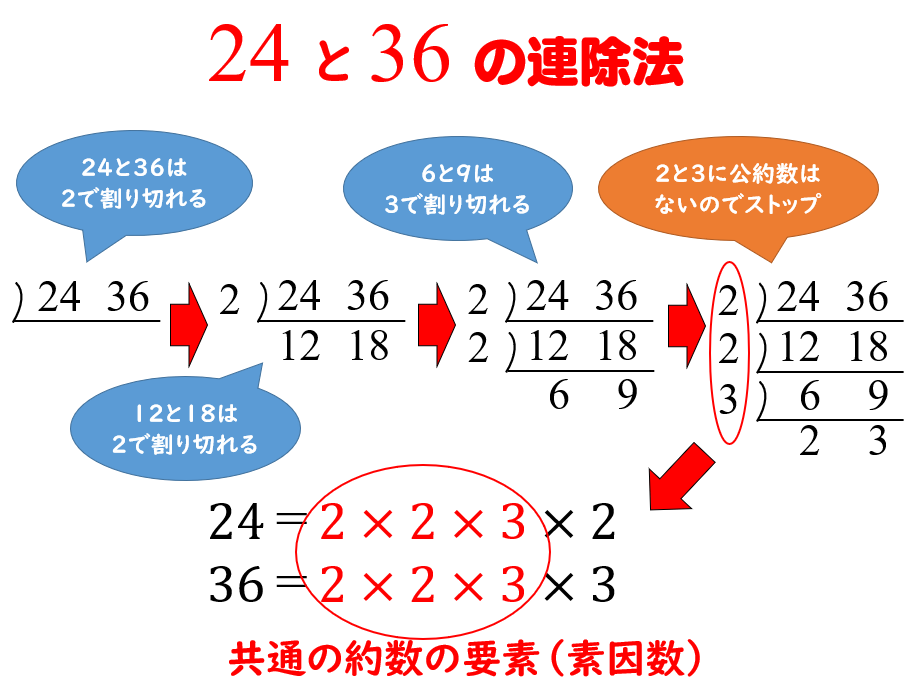
共通する素因数がなくなったところで終わりである\ {割った素因数の積が最大公約数}となる ならば,\ 210と462の両方を割り切る最も大きい数が42であることが求まったことになる 素因数分解の場合とは異なり,\ 小さい素数から順に割っていく必要はない 公約数の数を求められないからですよ。 公約数の個数を求める問題だって連除法で求めますからね。 鼻垂らした小学生に 「いい!公約数の個数を求めるときは素数ヨ!最大公約数だったら素数じゃなくていいから!場合分けして覚えてネ!



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



1




この素因数分解を利用した問題についてなのですが Clear




最大公約数と最小公倍数を求める 2 3 素因数分解を利用する 自由研究ノート 仮




高校数学a 最大公約数の求め方 例題編 映像授業のtry It トライイット




中学3年数学 最大公約数と最小公倍数 素因数分解の利用 Youtube




2 を赤ちゃんでもわかるくらい簡単に教えてください Clear



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




最大公約数と最小公倍数 オモワカ整数 4 全21回 数学専門塾met Note



数学の問題です 次の数の最大公約数の求め方をユークリッドを使わずに 下記 Yahoo 知恵袋




公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




小5 算数 小5 約数 公約数 最大公約数 Youtube



最小公倍数 最大公約数の求め方はこれでいいんですか 素因数分解は Yahoo 知恵袋




問題 素因数分解と公約数の基本 中学数学 理科 寺子屋塾の復習サイト




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場




最小公倍数って何 その求め方と素因数分解のテクニック アタリマエ




高校数学a 最小公倍数をヒントにnを求める問題 練習編 映像授業のtry It トライイット
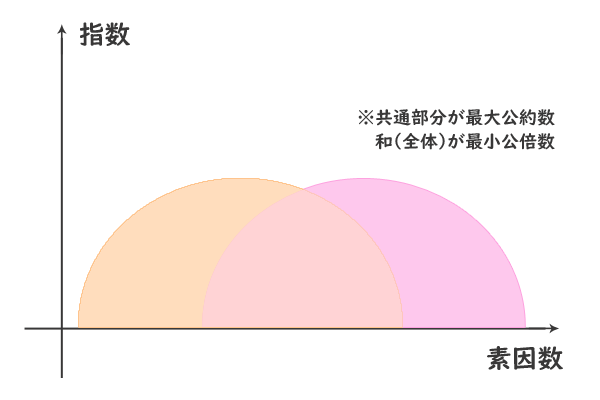



最大公約数と最小公倍数の計算方法 高校数学マスター



1




中学数学3年 公約数と最大公約数 受験の月




整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




競プロ 素因数分解と約数と倍数 なかけんの数学ノート




素因数分解による最大公約数 最小公倍数の求め方 中1数学 Youtube



2つの整数の最大公約数 最小公倍数と 3つの整数の最大公 Yahoo 知恵袋



3



U9j580gf8iba369ji2w Xyz P 1542




素因数分解のやり方のコツとは 応用問題3選も簡単に解けます 遊ぶ数学



数学の素因数分解についてプリントに60 84 90の最大公約数 Yahoo 知恵袋
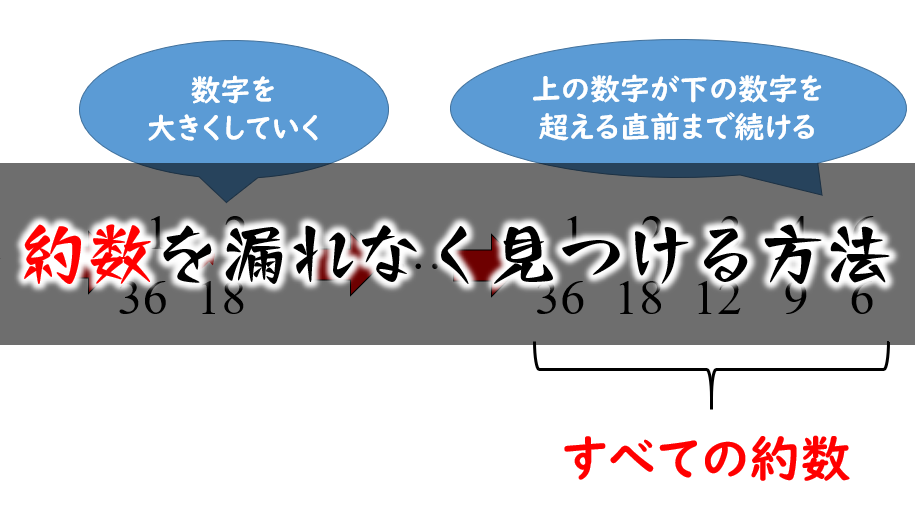



約数を漏れなく簡単に見つける方法 小学生でも素因数分解ができると便利 数学fun




中学3年数学 式の展開と因数分解 最大公約数と最小公倍数 練習問題2 解答 あんのん塾




最大公約数と最小公倍数のひみつ 苦手な数学を簡単に
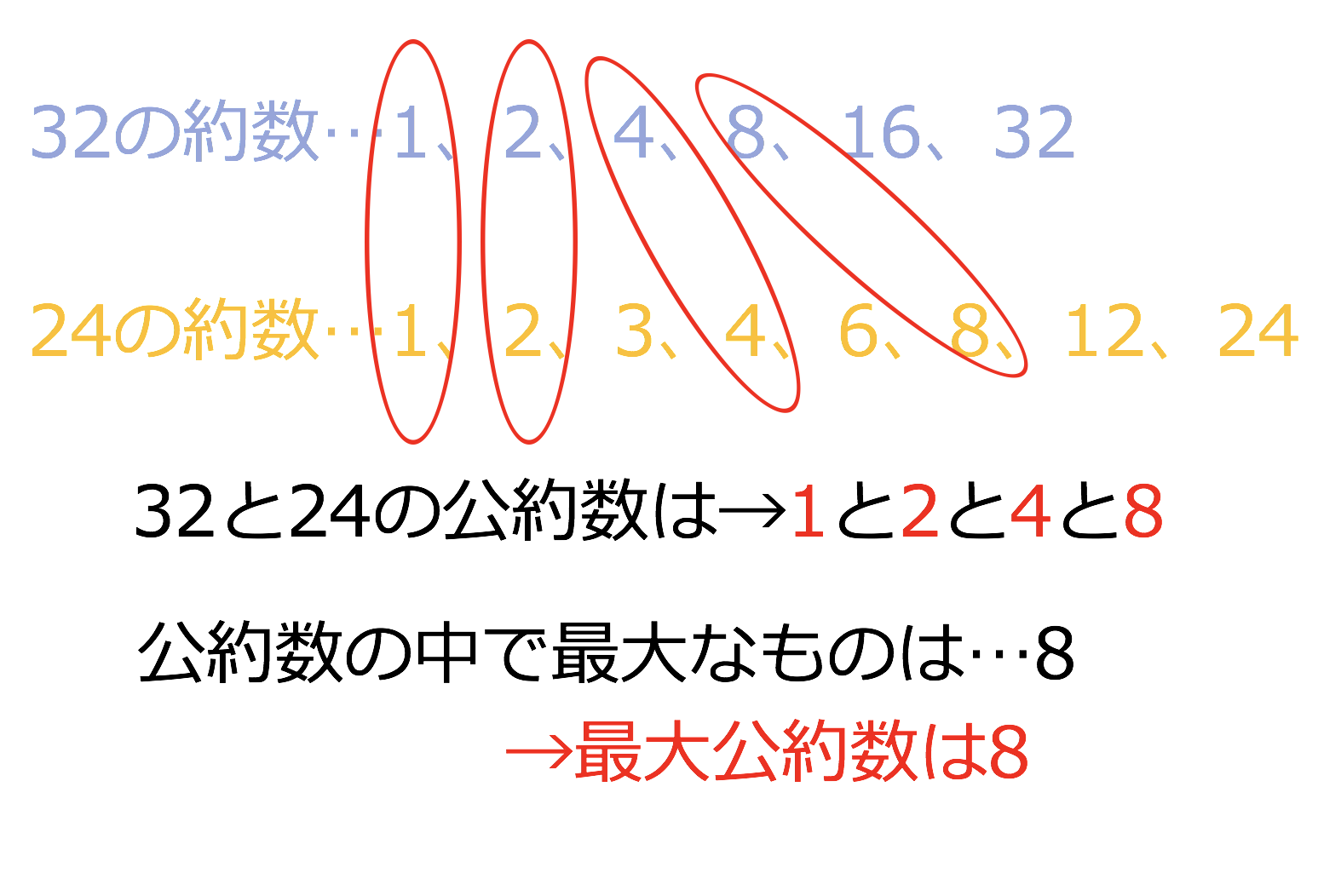



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




公約数 公倍数の求め方 Z Square Z会




高1です 数学がわかりません 教えてください 最大公約数と最小公 その他 学校 勉強 教えて Goo
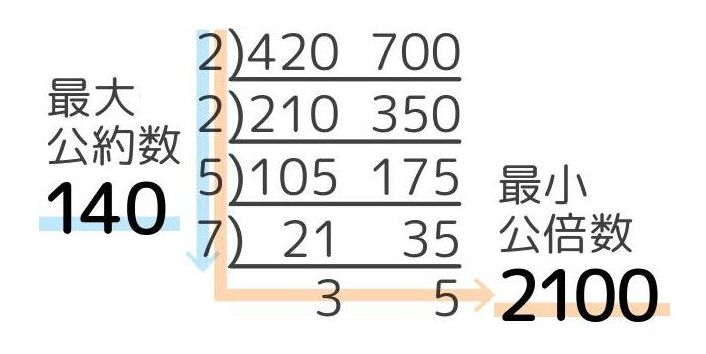



素因数分解と最小公倍数 最大公約数の求め方 小学生も中学生も 2つの数のすだれ算 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算




公約数 公倍数の求め方 Z Square Z会



素因数分解のドリル




中学受験 約数の個数の求め方は 素因数分解を活用すれば簡単です そうちゃ式 受験算数 新1号館 数論 特殊算
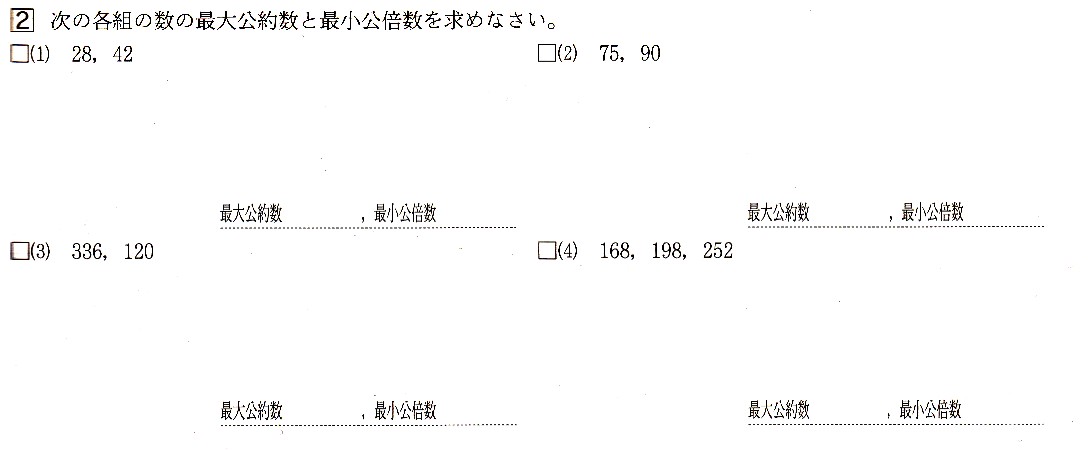



中学3年数学 式の展開と因数分解 最大公約数と最小公倍数 確認問題2 あんのん塾



数学i Aチェック リピート 第6章 3整数の性質 2 最大公約数 最小公倍数 Pukiwiki




最高の公倍数 公約 数 子供のための最高のぬりえ




中学3年数学 最大公約数と最小公倍数 素因数分解の利用 Youtube




16 同志社大 最大公約数 最小公倍数 不定方程式 数学のコツ壺 風いま数学協室




コがわからないです なぜ最大公約数 最小公倍数を素因数分解するのか Clear
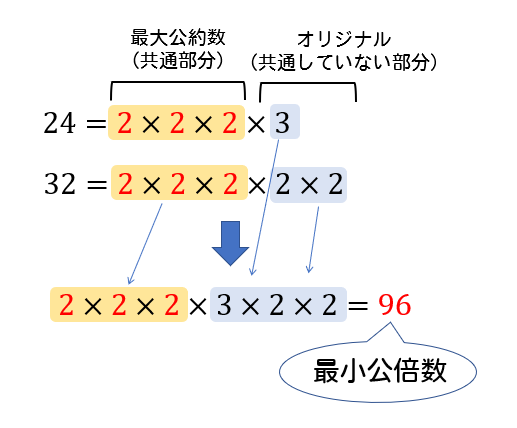



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




高校数学a 最大公約数と最小公倍数の定義 受験の月




素因数分解と最小公倍数 最大公約数の求め方 小学生も中学生も 2つの数のすだれ算 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算




最大公約数と最小公倍数の積の性質の2通りの証明 高校数学の美しい物語




整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
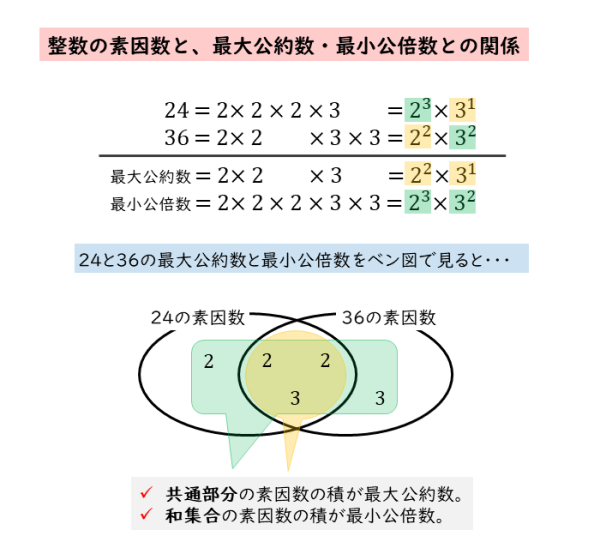



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




中学数学3年 素因数分解の応用 約数の個数 平方数 受験の月



最大公約数と最小公倍数
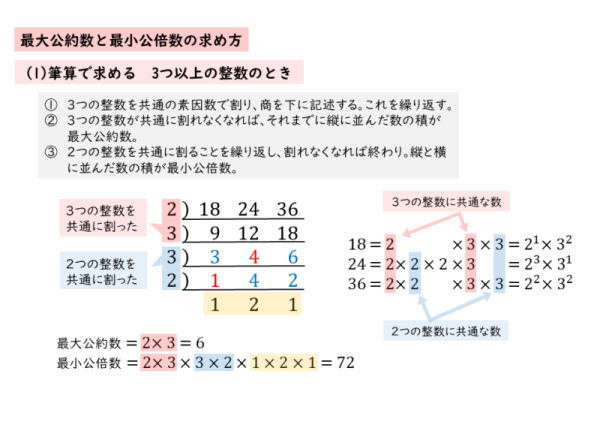



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



3




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




中1 1学期 整数の性質 素因数分解 のわかりやすい教え方 教える手順 ノートのとらせ方 問題もあります ヒカリブログ ワーママhikariの目からウロコ



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




中学受験 公 倍数 公 約数の基礎から応用問題まで全部まとめ そうちゃ式 受験算数 新1号館 数論 特殊算




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座



最大公約数と最小公倍数




素因数分解と最小公倍数 最大公約数の求め方 小学生も中学生も 2つの数のすだれ算 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算



素因数分解と最大公約数 最小公倍数 Gamesprit




最大公約数と最小公倍数を求める 2 3 素因数分解を利用する 自由研究ノート 仮



素因数分解を利用して 最大公約数と最小公倍数は求めることがで Yahoo 知恵袋




3つの数の素因数分解で最大公約数と最大公倍数を求める問題なのですが これってどこが間 Clear




中学3年数学 式の展開と因数分解 最大公約数と最小公倍数 確認問題3 あんのん塾




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




16 24 を素因数分解して この3つの数の Clear




小学5年生 算数 8月 約数と公約数 公倍数 公約数の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




24と180の最小公倍数 最大公約数を求める問題で 写真に書いてあるやり方でも解けま Clear
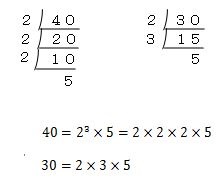



最大公約数の求め方 もう一度やり直しの算数 数学




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座




算数 最大公約数の求め方 素因数分解を使って 中学受験 Youtube




はじめての可換環 整数 17 素因数分解と最大公約数 Youtube




最大公約数と最小公倍数の関係 Youtube




は36 108 Clear




3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




中学数学より4 教科書に登場しない最小公倍数 最大公約数 身勝手な主張



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



整数の性質の問題です 以下の問題の解説をお願いします 素因数分解するの Yahoo 知恵袋



最小公倍数 最大公約数のドリル



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典




競プロ 素因数分解と約数と倍数 なかけんの数学ノート



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿